Spațiu Hausdorff
Un spațiu Hausdorff este un spațiu topologic în care orice două puncte distincte pot fi separate prin vecinătăți deschise care nu se suprapun. Această proprietate asigură că fiecare punct poate fi identificat clar și fără ambiguități.
Pe scurt, într-un spațiu Hausdorff, pentru două puncte diferite \( x \) și \( y \), putem găsi întotdeauna două vecinătăți deschise \( U \) și \( V \) astfel încât acestea să fie complet disjuncte, adică \( U \cap V = \emptyset \). Aceasta transpune în limbaj matematic ideea intuitivă de „separare” pe care o avem în spațiile geometrice familiare.
Spațiile Hausdorff sunt esențiale în analiză și topologie deoarece permit o tratare coerentă a convergenței șirurilor și a altor concepte de bază. În plus, în orice spațiu Hausdorff, orice mulțime formată dintr-un singur punct este închisă. Motivul este simplu: complementul său este o mulțime deschisă.
Exemple
Exemplul 1
Considerăm topologia standard a dreptei reale \(\mathbb{R}\), folosită în mod obișnuit ca model în matematică.

În această topologie, punctele singulare nu sunt deschise.
Explicație: Pentru ca o mulțime să fie deschisă în topologia standard, fiecare punct al ei trebuie să aibă în jur un interval deschis complet. Un singur punct \( \{x\} \) nu poate conține un astfel de interval, așa că nu poate fi deschis. Prin urmare, punctele individuale nu sunt deschise în \(\mathbb{R}\).
Complementul unui punct \( \mathbb{R} \setminus \{x\} \), în schimb, este întotdeauna deschis. Aceasta arată că un punct izolat este o mulțime închisă.

Topologia standard este un exemplu clasic de spațiu Hausdorff. Pentru două puncte diferite \( a \) și \( b \), putem găsi intervale deschise disjuncte care le separă.
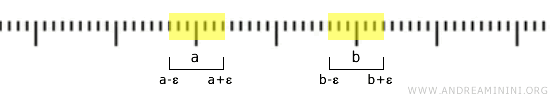
Dacă \( a < b \), alegem intervalele \( (a-\epsilon, a+\epsilon) \) și \( (b-\epsilon, b+\epsilon) \). Dacă \( \epsilon \) este suficient de mic astfel încât \( a+\epsilon < b-\epsilon \), cele două intervale sunt complet separate.
Această proprietate confirmă că \(\mathbb{R}\), cu topologia sa uzuală, este un spațiu Hausdorff.
Exemplul 2
Să privim acum un exemplu mai simplu: mulțimea \( X = \{1,2,3\} \), echipată cu topologia discretă.
În topologia discretă, orice submulțime este deschisă. Fiecare punct este, prin definiție, o mulțime deschisă.
Iată toate mulțimile deschise posibile:
- \( \emptyset \)
- \( \{1\}, \{2\}, \{3\} \)
- \( \{1,2\}, \{1,3\}, \{2,3\} \)
- \( \{1,2,3\} \)
În total avem \( 2^3 = 8 \) submulțimi, iar toate sunt deschise.
Acest spațiu este întotdeauna un spațiu Hausdorff deoarece pentru două puncte diferite \( x \) și \( y \) putem lua vecinătățile simple \( \{x\} \) și \( \{y\} \), care sunt deja deschise și, evident, disjuncte.
De exemplu:
$$ \{1\} \cap \{2\} = \emptyset $$
Prin urmare, orice două puncte pot fi separate în mod direct.
Deschise sau închise?
La prima vedere ar părea ciudat că în topologia discretă, mulțimile unitare \( \{x\} \) sunt în același timp deschise și închise. Dar acest lucru nu este deloc neobișnuit în topologie.
O mulțime poate fi simultan deschisă și închisă. Astfel de mulțimi se numesc clopen.
În topologia discretă, o mulțime \( \{x\} \) este deschisă prin definiție. Complementul ei, fiind și el o mulțime deschisă, face ca \( \{x\} \) să fie și închisă.
Exemplu: pentru \( X = \{1,2,3\} \), mulțimea \( \{1\} \) este deschisă, iar complementul ei \( \{2,3\} \) este de asemenea deschis. Prin urmare, \( \{1\} \) este închisă.
- Deschise
Orice punct este o mulțime deschisă în topologia discretă. - Închise
Complementul fiecărui punct este deschis, ceea ce face ca punctul însuși să fie închis.
Astfel, în topologia discretă, punctele sunt simultan deschise și închise. Acesta este unul dintre motivele pentru care acest tip de topologie este atât de ușor de analizat.
Observații esențiale
Demonstrație pe scurt: Considerăm un șir \( x_1, x_2, x_3, \dots \) care ar converge simultan la \( x \) și \( y \), cu \( x \neq y \). Există un rang \( N \) pentru care \( x_n \) este în orice vecinătate a lui \( x \) atunci când \( n > N \). În mod similar, există un rang \( M \) pentru vecinătățile lui \( y \). Dacă \( M > N \), unele elemente ale șirului ar aparține simultan ambelor vecinătăți, ceea ce ar contrazice separarea Hausdorff. Prin urmare, un șir nu poate avea două limite diferite.
- Unicitatea limitei
Într-un spațiu Hausdorff, orice șir convergent are o singură limită. Dacă un șir ar avea două limite posibile, vecinătățile corespunzătoare s-ar suprapune, ceea ce ar încălca axioma Hausdorff.