Transformări topologice

Transformările topologice sunt operații aplicate spațiilor matematice care păstrează proprietăți fundamentale precum conectivitatea și continuitatea. Cu alte cuvinte, ele arată cum un obiect poate fi deformat fără să se rupă sau să fie lipit la loc.

Topologia este adesea numită „geometria din cauciuc", pentru că se ocupă de proprietățile care rămân neschimbate atunci când întindem, comprimăm sau îndoim un obiect. Cât timp nu-l rupem și nu-l lipim, pentru topolog, forma rămâne aceeași.

Principalele trăsături ale transformărilor topologice sunt:

• Continuitatea
  Transformarea trebuie să fie lină și fără salturi: mici modificări ale unei forme duc la mici modificări ale celeilalte.
• Conectivitatea
  Dacă două puncte erau conectate sau apropiate înainte de transformare, ele rămân la fel și după.
• Deformarea fără rupturi
  Poți întinde, comprima sau răsuci obiectul, dar nu-l poți rupe sau lipi. Exemplul clasic: o gogoașă poate fi transformată într-o ceașcă de cafea - ambele au un singur gol.

Aplicații: Transformările topologice sunt folosite nu doar în matematică, ci și în fizică, informatică și chiar biologie, pentru a studia structuri care își păstrează esența chiar și când forma se schimbă.

Tipuri principale de transformări topologice

Topologia clasifică transformările în funcție de ce proprietăți păstrează. Cele mai importante sunt:

• Homeomorfisme
  Sunt transformări continue care pot fi inversate tot printr-o transformare continuă. Practic, permit „modelarea" unui obiect în altul fără rupturi. Exemplu: ceașca și gogoasa - două forme diferite, dar topologic echivalente.
• Izotopii
  Reprezintă serii de homeomorfisme succesive. Imaginează-ți un nod care se mișcă de-a lungul unei frânghii fără a fi strâns sau desfăcut - fiecare poziție intermediară este o izotopie.
• Homotopii
  Descriu cum o funcție se poate deforma într-o alta fără a pierde continuitatea. Este o noțiune mai flexibilă decât homeomorfismul. De exemplu, întinderea și relaxarea unui arc sunt două forme homotopice între ele.
• Difeomorfisme
  Acestea sunt transformări continue și derivabile - adică „fine" din punct de vedere matematic. Sunt fundamentale în topologia diferențială, unde contează netezimea suprafețelor, cum ar fi transformarea unei sfere elastice într-un elipsoid.

Fiecare tip de transformare surprinde un mod diferit de a înțelege cum se poate modifica un spațiu fără a-i schimba natura profundă. Alegerea depinde de domeniul de studiu: topologie generală, algebrică sau diferențială.

Transformări geometrice vs. transformări topologice

Deși par asemănătoare, transformările geometrice și cele topologice urmăresc scopuri diferite:

• Transformările geometrice
  Păstrează dimensiuni, unghiuri și distanțe. Exemple: translații, rotații, reflexii sau scalări.

  O rotație, de exemplu, păstrează distanțele și unghiurile, dar schimbă orientarea obiectului.

• Transformările topologice
  Ignoră măsurile exacte și se concentrează pe continuitate și conectivitate. Ele pot schimba complet forma, atâta timp cât nu există tăieturi sau lipiri.

  De exemplu, topologia acceptă că o gogoașă și o ceașcă sunt același obiect - ambele au un singur gol.

Pe scurt, transformările geometrice sunt despre măsură și proporție, în timp ce transformările topologice sunt despre relații și structură - despre ce rămâne neschimbat atunci când totul se schimbă.

Transformări care sunt și geometrice, și topologice

Există și transformări care aparțin ambelor lumi. Ele modifică poziția sau orientarea obiectelor, dar rămân continue și păstrează conectivitatea.

• Izometrii
  Translațiile, rotațiile și reflexiile păstrează distanțele și unghiurile - sunt transformări simultan geometrice și topologice, pentru că au invers continuu.
  
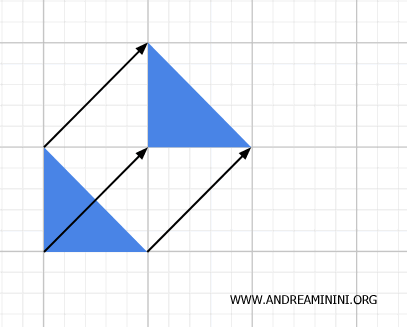
• Similitudini
  Acestea schimbă dimensiunea unui obiect, dar păstrează forma și proporțiile. Sunt transformări geometrice prin efectul asupra mărimii, dar și topologice, pentru că rămân continue și nu distrug conectivitatea.

Astfel, geometria și topologia nu se exclud. Dimpotrivă, ele se completează: una se ocupă cu forma și măsura, cealaltă cu esența și relațiile dintre părțile unui spațiu.

Topologia ne învață că, dincolo de aparențe, uneori două forme complet diferite pot fi - în profunzime - aceleași.