Interiorul unei mulțimi
Într-un spațiu topologic \( X \), interiorul unei mulțimi \( A \) este definit ca reuniunea tuturor submulțimilor deschise care se află în întregime în \( A \). Notațiile consacrate sunt \( \text{Int}(A) \) și \( A^\circ \).
Interiorul este, așadar, cea mai mare mulțime deschisă inclusă integral în \( A \). Este partea din \( A \) unde toate punctele au suficient spațiu în jurul lor, în sens topologic, pentru a rămâne complet în interiorul mulțimii.
Nicio altă mulțime deschisă inclusă în \( A \) nu o poate depăși ca întindere.
Observație: Pentru că este construit din reuniunea unor mulțimi deschise, interiorul este automat o mulțime deschisă. Această proprietate nu depinde de forma lui \( A \), ci de structura topologică a spațiului.
Formal, interiorul lui \( A \) este ansamblul punctelor care dispun de un vecinaj deschis aflat în întregime în interiorul lui \( A \):
$$ \text{Int}(A) = \bigcup \{ U \subseteq A : U \text{ este deschis în } X \} $$
Un punct \( x \) aparține interiorului dacă există o mulțime deschisă \( U \) cuprinsă în \( A \) care îl conține pe \( x \). Această condiție exprimă ideea de acces liber la un vecinaj complet „protejat” de marginea lui \( A \).
Observație: Interiorul unei mulțimi nu ține doar de mulțimea în sine, ci de topologia în care este plasată. O schimbare a topologiei poate modifica radical interiorul.
Exemplu
Considerăm mulțimea \( A = [0,1] \) din \( \mathbb{R} \), cu topologia obișnuită. Intervalul include toate valorile între 0 și 1, cu tot cu capete.
Interiorul său este:
$$ \text{Int}(A) = (0,1) $$
Punctele 0 și 1 nu pot aparține niciunui interval deschis complet inclus în \( A \), ceea ce explică absența lor din interior.
Exemplul 2
Analizăm acum mulțimea \( A = [0,1) \), deci închisă la stânga și deschisă la dreapta. În ciuda acestei diferențe, interiorul rămâne același:
\[ \text{Int}(A) = (0,1) \]
Motivul este simplu: intervalul \( (0,1) \) este în continuare cea mai mare mulțime deschisă inclusă în \( A \).
Observație: În topologia standard, deschisele sunt reuniuni de intervale deschise. Cum 0 nu poate aparține niciunui astfel de interval complet inclus în \( [0,1) \), el este automat exclus din interior.
Exemplul 3
Să revenim la aceeași mulțime \( [0,1) \), dar privită acum într-un spațiu cu topologia discretă. Aici, orice submulțime este deschisă prin definiție, ceea ce face noțiunea de interior mult mai directă.
Rezultatul este:
$$ \text{Int}(A) = A = [0,1) $$
Fiecare punct dispune de propriul său vecinaj deschis, iar mulțimea întreagă este deschisă.
Observație: Acest caz arată cât de diferită poate fi noțiunea de interior în funcție de topologie. În discretă, toate mulțimile sunt deschise, deci interiorul este întotdeauna mulțimea însăși.
Exemplul 4
Considerăm spațiul finit \( X = \{a, b, c\} \), tot cu o topologie discretă. Toate submulțimile sunt deschise, de la mulțimea vidă până la mulțimea totală.
- \( \emptyset \) și \( \{a, b, c\} \) sunt deschise.\setminus
- Singletonurile \( \{a\} \), \( \{b\} \), \( \{c\} \) sunt deschise.
- Submulțimile cu două elemente sunt, la rândul lor, deschise.
Pentru mulțimea \( A = \{b, c\} \), interiorul este:
\[ \text{Int}(A) = \{b\} \cup \{c\} \cup \{b, c\} = \{b, c\} \]
Interiorul coincide cu mulțimea însăși, așa cum se întâmplă în orice spațiu cu topologie discretă.
Observație: În topologia discretă, proprietățile interioarelor devin transparente. Fiecare submulțime este deschisă, iar interiorul ei reflectă exact acest fapt.
Teorema interiorului unei mulțimi
Într-un spațiu topologic \( X \), o submulțime \( S \subseteq X \) și un punct \( y \in X \), spunem că \( y \) aparține interiorului lui \( S \), notat \( \operatorname{Int}(S) \), dacă există o mulțime deschisă \( U \) cu proprietatea că \( y \in U \subseteq S \). Formal: $$ y \in \operatorname{Int}(S) \iff \exists\, U \text{ deschis, cu } y \in U \subseteq S. $$
Ideea este simplă: un punct se află în interiorul unei mulțimi dacă „are loc" în jurul său, adică dacă poate fi înconjurat de un vecinaj deschis care rămâne complet în interiorul mulțimii. Interiorul surprinde acea porțiune a mulțimii în care nu apar influențe ale frontierei.
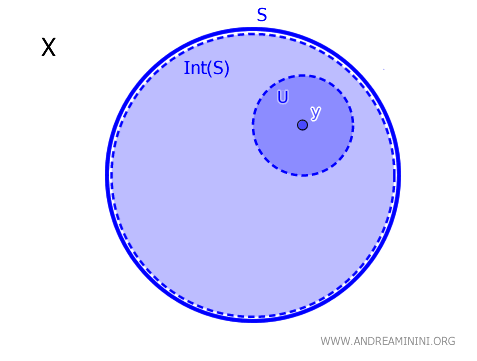
Teorema oferă astfel un criteriu clar și eficient pentru a stabili dacă un punct este interior într-un spațiu topologic.
Demonstrație
- Condiția necesară: Dacă un punct este interior, atunci există întotdeauna un deschis care îl conține și care nu părăsește mulțimea. Aceasta derivă direct din definiție.
- Condiția suficientă: Dacă găsim un deschis inclus în mulțime care conține punctul, atunci punctul este interior. Interiorul reunește toate aceste deschise, deci criteriul este imediat satisfăcut.
Observație: Teorema precizează exact relația dintre deschise și interior. Este un instrument esențial în studiul continuității și al structurii topologice.
Exemplu
Să analizăm mulțimea \( A = [1,3] \subset \mathbb{R} \), intervalul închis între 1 și 3, în topologia standard.
$$ A = [1,3] $$
Pentru a afla interiorul, aplicăm criteriul anterior.
Determinarea interiorului lui \( A \)
- Alegerea unui deschis
Un candidat natural este intervalul deschis \( (1,3) \), singurul deschis maximal aflat complet în interiorul lui \( [1,3] \). - Verificarea incluziunii
Intervalul \( (1,3) \) se află în totalitate în \( [1,3] \). Punctele 1 și 3 rămân pe frontieră și nu pot face parte din interior.
Rezultatul este clar: $$ \operatorname{Int}(A) = (1,3). $$
Observație: Frontiera intervalului, formată din punctele 1 și 3, nu admite vecinaje deschise incluse în \( A \), ceea ce explică excluderea lor din interior.
Proprietăți ale interiorului
Interiorul unei mulțimi este un operator cu un comportament bine structurat. Proprietățile de mai jos sunt printre cele mai folosite în topologie și ajută la înțelegerea modului în care interiorul interacționează cu operații precum reuniunea, intersecția sau complementarea.
- Reuniunea interioarelor
Pentru două mulțimi \( A \) și \( B \), avem: $$ \operatorname{Int}(A) \cup \operatorname{Int}(B) \subseteq \operatorname{Int}(A \cup B). $$ În multe situații, incluziunea este strictă. - Interiorul intersecției
În contrast cu cazul reuniunii: $$ \operatorname{Int}(A \cap B) = \operatorname{Int}(A) \cap \operatorname{Int}(B), $$ o proprietate elegantă și perfect simetrică. - Interiorul complementului și aderența
Există o legătură puternică între interior și aderență: $$ \operatorname{Int}(X - A) = X - \operatorname{Cl}(A). $$ - Aderența complementului
Dual, se verifică: $$ \operatorname{Cl}(X - A) = X - \operatorname{Int}(A). $$
Observații
Mai jos regăsim câteva observații esențiale care completează înțelegerea operatorului interior:
- Orice mulțime deschisă inclusă într-o mulțime este inclusă și în interiorul acesteia
Acest lucru reflectă faptul că interiorul este cel mai mare deschis cuprins în mulțime. - Interiorul este monoton
Dacă \( A \subseteq B \), atunci: $$ \operatorname{Int}(A) \subseteq \operatorname{Int}(B). $$ - Caracterizarea mulțimilor deschise
O mulțime este deschisă dacă și numai dacă coincide cu interiorul său: $$ A = \operatorname{Int}(A). $$ - Determinarea interiorului cu R
Limbajul R oferă mijloace utile pentru explorarea vizuală și analitică a interiorului mulțimilor.
Aceste idei formează fundația conceptuală a operatorului interior și sunt indispensabile pentru o înțelegere solidă a topologiei moderne.