Uniunea interiorurilor a două mulțimi
Uniunea interiorurilor mulțimilor \( A \) și \( B \) este întotdeauna inclusă în interiorul uniunii lor: \[ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) \] Totuși, această relație nu duce în mod necesar la o egalitate. Această diferență aparent subtilă joacă un rol important în înțelegerea structurii mulțimilor într-un spațiu topologic.
Pe scurt, interiorul uniunii este întotdeauna cel puțin la fel de mare ca uniunea interiorurilor. Dar, în multe situații, cele două nu coincid.
Afirmația:
$$ \text{Int}(A) \cup \text{Int}(B) = \text{Int}(A \cup B) $$
nu este universal valabilă. De fapt, în numeroase cazuri, includerea este una strictă:
$$ \text{Int}(A) \cup \text{Int}(B) \ne \text{Int}(A \cup B) $$
Această observație ne ajută să înțelegem mai bine modul în care interiorul unei mulțimi reacționează la operațiile setuale.
Exemplu ilustrativ
Să începem cu două intervale deschise din \(\mathbb{R}\):
$$ A = (0, 2) \qquad B = (1, 3) $$
Interiorul unui interval deschis este intervalul însuși:
$$ \text{Int}(A) = (0, 2), \quad \text{Int}(B) = (1, 3) $$
Uniunea interiorurilor este:
$$ (0, 2) \cup (1, 3) = (0, 3) $$
Iar uniunea mulțimilor coincide cu același interval:
$$ A \cup B = (0, 3) $$
Deci:
$$ \text{Int}(A \cup B) = (0, 3) $$
În această situație, cele două părți sunt egale.
În schimb, dacă luăm două intervale închise: $$ A = [0, 2], \quad B = [2, 3] $$ interioarele sunt $$ (0, 2), \quad (2, 3) $$ iar interiorul uniunii este $$ (0, 3) $$ Aici, punctul \( 2 \) aparține interiorului uniunii, dar nu interiorului vreunui interval individual. Prin urmare, uniunea interiorurilor: $$ (0, 2) \cup (2, 3) $$ este strict mai mică decât interiorul uniunii.
Exemplul 2
Dacă intervalele sunt deschise și disjuncte:
$$ A = (0, 1), \quad B = (2, 3) $$
interioarele rămân aceleași, iar uniunea lor este deja deschisă:
$$ A \cup B = (0, 1) \cup (2, 3) $$
De această dată, interiorul uniunii coincide cu uniunea interiorurilor.
Aceste exemple arată că egalitatea poate apărea, dar nu este garantată. Totul depinde de modul în care mulțimile se întâlnesc la margini.
Exemplul 3: două discuri în plan
Să trecem acum în \(\mathbb{R}^2\), unde mulțimile capătă forme geometrice mai vizibile. Considerăm două discuri deschise care se suprapun parțial:
$$ A = \{ (x, y) \mid x^2 + y^2 < 1 \} $$
$$ B = \{ (x, y) \mid (x - 0{,}5)^2 + y^2 < 1 \} $$
Fiind deschise, interiorul lor coincide cu mulțimile însele. Uniunea interiorurilor este deci:
$$ A \cup B $$
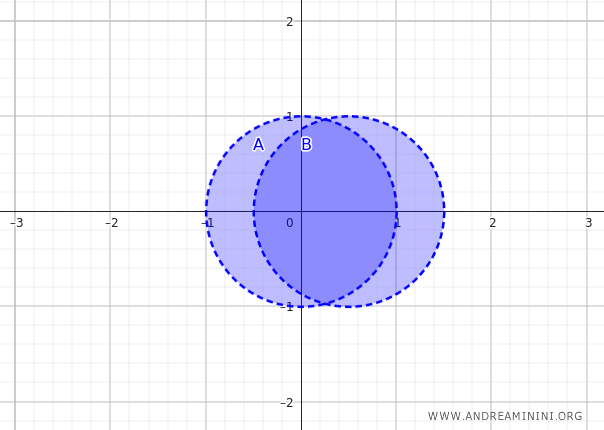
Interiorul uniunii este aceeași regiune: orice punct are în jur un vecinaj complet inclus în \( A \cup B \).
Și aici se verifică relația generală:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Demonstrarea proprietății
Pentru a justifica riguros această proprietate, pornim de la definiția interiorului.
Interiorul unei mulțimi \( X \), notat \( \text{Int}(X) \), reprezintă mulțimea punctelor care admit un vecinaj complet inclus în \( X \).
Luăm un punct \( x \in \text{Int}(A) \cup \text{Int}(B) \). Atunci \( x \) aparține interiorului uneia dintre mulțimi.
- Dacă \( x \in \text{Int}(A) \), există un deschis \( U_x \) cu \( x \in U_x \subseteq A \).
- Dacă \( x \in \text{Int}(B) \), există un deschis \( V_x \) cu \( x \in V_x \subseteq B \).
În ambele cazuri, deschisul respectiv este inclus și în uniunea \( A \cup B \). Prin urmare, punctul se află și în interiorul uniunii.
Obținem astfel concluzia naturală și generală:
$$ \text{Int}(A) \cup \text{Int}(B) \subseteq \text{Int}(A \cup B) $$
Această proprietate este fundamentală pentru modul în care interiorul interacționează cu operațiile pe mulțimi într-un spațiu topologic. Ea surprinde o idee simplă, dar extrem de utilă: interiorul unei uniuni nu poate fi „mai mic” decât interiorurile mulțimilor din care este compusă.