Topologia discretă
Topologia discretă \( T \) este cea mai fină topologie care se poate defini pe o mulțime \( X \), deoarece include toate submulțimile acesteia. Este, prin urmare, un caz extrem: nimic nu poate fi „mai deschis” decât o topologie discretă.
Într-o astfel de structură, familia mulțimilor deschise \( T \) cuprinde toate submulțimile lui \( X \). Cu alte cuvinte, fiecare submulțime a lui \( X \) este considerată deschisă prin definiție.
Consecința este simplă, dar importantă: fiecare element al lui \( X \) formează o mulțime deschisă în sine. Fiecare punct este complet izolat, fără nicio legătură de vecinătate cu celelalte.
Prin urmare, într-o topologie discretă, nu există noțiunea de „apropiere” sau „continuitate” între puncte. Fiecare element există separat, fără restricții privind modul în care este „plasat” în spațiu.
Observație. O topologie pe o mulțime \( X \) este o colecție de submulțimi (numite deschise) care îndeplinesc trei condiții de bază:
- Mulțimea vidă și întreaga mulțime \( X \) aparțin colecției \( T \).
- Uniunea arbitrară a mulțimilor din \( T \) aparține tot lui \( T \).
- Intersecția finită a mulțimilor din \( T \) aparține, de asemenea, lui \( T \).
Se numește discretă pentru că tratează fiecare element al lui \( X \) ca fiind complet independent. În această topologie, nu există legături între puncte și nici noțiunea de „continuitate” spațială.
Este cea mai bogată topologie posibilă, deoarece nicio altă topologie nu poate conține mai multe mulțimi deschise: aceasta le include pe toate.
Observație. Aceste reguli formează baza studiului topologic al mulțimilor deschise și oferă un cadru formal pentru a înțelege cum pot fi percepute conceptele de „apropiere” și „continuitate” - idei esențiale în analiza spațiilor topologice.
O proprietate interesantă a topologiei discrete este următoarea:
În topologia discretă, orice submulțime a unui spațiu topologic este în același timp deschisă și închisă.
Motivul este simplu: dacă toate submulțimile sunt deschise, atunci și complementarele lor - care sunt tot submulțimi - vor fi deschise. Prin definiție, o mulțime este închisă dacă complementara ei este deschisă. Prin urmare, toate submulțimile sunt automat și închise.
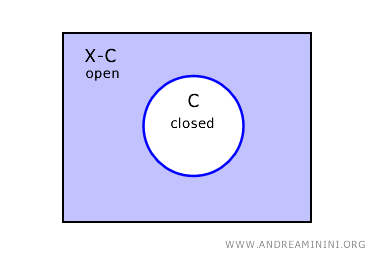
Această proprietate face ca fiecare submulțime dintr-un spațiu discret să fie o mulțime clopen, adică simultan deschisă și închisă. Este o situație unică în topologie, valabilă fără nicio excepție.
Observație. În topologia discretă, nu doar punctele izolate, ci toate submulțimile se bucură de această proprietate. Fiecare punct este o mulțime deschisă, iar orice combinație de puncte este la rândul ei deschisă. Cum complementara oricărei submulțimi este tot o submulțime a lui \( X \), deci o mulțime deschisă, rezultă că fiecare submulțime este și închisă.
Exemplu practic
Pentru a înțelege mai bine conceptul, să considerăm o mulțime finită \( X \) formată din trei elemente:
$$ X = \{a, b, c\} $$
Mulțimea părților lui \( X \), adică totalitatea submulțimilor sale posibile, este:
- Mulțimea vidă: \(\emptyset\)
- Mulțimile unitare: \(\{a\}\), \(\{b\}\), \(\{c\}\)
- Submulțimile cu două elemente: \(\{a, b\}\), \(\{a, c\}\), \(\{b, c\}\)
- Mulțimea totală: \(\{a, b, c\}\)
În topologia discretă definită pe \( X \), fiecare dintre aceste submulțimi este o mulțime deschisă. Astfel, topologia \( T \) poate fi scrisă ca:
$$ T = \{\emptyset, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\} $$
Prin definiție, toate aceste submulțimi sunt deschise. Prin urmare, topologia este completă și respectă toate condițiile formale: conține mulțimea vidă, întreaga mulțime \( X \) și este stabilă la uniuni arbitrare și intersecții finite.
Să analizăm, de exemplu, submulțimea \( \{ a \} \). Aceasta este deschisă prin definiție. Complementara sa, \( X \setminus \{a\} = \{b, c\} \), este tot o mulțime deschisă, deci \( \{ a \} \) este și închisă. Prin urmare, în topologia discretă, orice submulțime este simultan deschisă și închisă.
Aceeași logică se aplică tuturor submulțimilor lui \( X \), fără excepție.