Bila deschisă

În topologie, o bilă deschisă - denumită, în funcție de context, vecinătate circulară, disc sau sferă deschisă - reprezintă mulțimea tuturor punctelor aflate la o distanță strict mai mică decât o valoare dată față de un punct fix, numit centru $ c $. Această valoare este raza $ r $: $$ B(c, r) = \{ x \in M \mid d(c, x) < r \} $$

Noțiunea își are locul într-un spațiu metric ($ M $), unde $ d $ este o metrică, funcția care stabilește distanța dintre două puncte și guvernează modul în care analizăm structura locurilor geometrice.

O bilă deschisă este complet determinată de centrul ei și de rază.

Este numită „deschisă" deoarece fiecare punct interior poate deveni centrul unei bile mai mici, inclusă în întregime în cea inițială. Această idee stă la baza modului în care topologia metrică descrie continuitatea.

Notă: Bilele deschise își păstrează proprietățile topologice chiar dacă sunt translatate sau scalate. Poziția sau dimensiunea nu modifică felul în care funcționează în cadrul topologiei.

În planul $ \mathbb{R}^2 $, distanța dintre un punct $ p = (x, y) $ și un punct $ c = (x_0, y_0) $, considerat centru, este calculată folosind metrica euclidiană:

$$ d(p,c) = \sqrt{(x-x_0)^2+(y-y_0)^2} $$

Bilele deschise stau la temelia topologiei standard a planului $ \mathbb{R}^2 $. Ele formează o bază pentru această topologie, ceea ce înseamnă că orice mulțime deschisă poate fi obținută prin reunirea unor astfel de bile.

Topologia standard este generată de mulțimea tuturor bilelor deschise:

$$ B = \{ B(p, r) \ | \ p \in \mathbb{R}^2, \ r > 0 \} $$

În această formulare, $ p $ este un punct din plan, iar $ r $ este o rază pozitivă.

baze de bile deschise în topologia standard pe R²

Deși există și alte topologii posibile pe $ \mathbb{R}^2 $, structura indusă de metrica euclidiană este cea mai folosită și oferă imaginea familiară a spațiului continuu.

Un aspect important este următorul: oricare ar fi punctul $ q \in B(p,r) $, există o rază $ \epsilon $ suficient de mică încât bila $ B(q,\epsilon) $ să fie inclusă în întregime în bila inițială. Acest lucru arată că interiorul unei bile deschise este stabil din punct de vedere topologic.

Formal, relația se exprimă astfel:

$$ \forall \ q \in B(p,r) \ \exists \ \epsilon > 0 \ \text{astfel încât} \ B(q,\epsilon) \subset B(p,r) $$

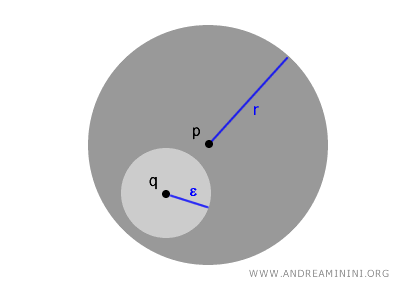
relația topologică dintre două bile deschise

Această structură în trepte - bile în interiorul altor bile - arată cât de fină este topologia indusă de metrică și explică modul în care putem analiza local spațiile continue.