Puncte fixe în topologie
În topologie, un punct fix este o valoare care nu se modifică atunci când aplicăm o funcție. Cu alte cuvinte, funcția „lasă în loc” acel punct.
Dacă avem o funcție f(x), spunem că un punct p este fix atunci când f(p) = p. Asta înseamnă că rezultatul funcției este exact același cu valoarea de la care am pornit.
$$ f(p) = p $$
Un exemplu intuitiv este rotația unui obiect în jurul unui punct central P.
În timpul rotației, toate punctele obiectului își schimbă poziția, în afară de centrul de rotație, care rămâne în același loc.
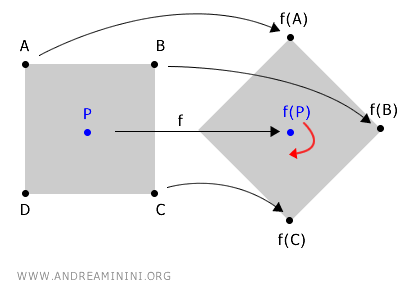
În acest caz, centrul de rotație P este un punct fix, deoarece funcția de rotație f(P) nu modifică coordonatele sale.
$$ f(P) \longrightarrow P $$
Ideea de punct fix are aplicații mult dincolo de topologie. O regăsim în analiză numerică, în teoria jocurilor, în economie și chiar în studiul sistemelor dinamice, unde ajută la identificarea stărilor de echilibru.
Un exemplu celebru este teorema punctului fix a lui Brouwer.
Exemplu practic
Să luăm funcția f(x) = sin(x) pe intervalul [0, 2π] radiani.
$$ f(x) = \sin(x) $$
Aici, punctul p = 0 radiani este un punct fix, deoarece sin(0) = 0. Funcția nu schimbă valoarea de intrare.
$$ \sin(0) = 0 $$
Rezultatul este identic cu valoarea inițială.
Exemplul 2
Considerăm acum funcția f(x) = cos(x) pe același interval [0, 2π].
$$ f(x) = \cos(x) $$
În acest caz, x = 0 nu este un punct fix, deoarece cos(0) = 1, deci valoarea de ieșire diferă de cea de intrare.
Totuși, funcția are un punct fix aproximativ la x = 0.73908513 radiani.
$$ \cos(0.73908513) = 0.73908513 $$
Valoarea obținută este practic aceeași cu cea introdusă, ceea ce confirmă existența punctului fix.
Teorema punctului fix a lui Brouwer
Această teoremă afirmă un lucru simplu, dar profund:
Orice funcție continuă care aplică un interval închis asupra lui însuși într-un spațiu de n dimensiuni are cel puțin un punct fix.
Este o teoremă de existență: garantează că un punct fix trebuie să existe, chiar dacă nu ne spune exact unde se află.
Rezultatul are consecințe importante. El stă la baza demonstrației existenței punctelor de echilibru în economie, în teoria jocurilor și în studiul sistemelor fizice sau biologice complexe.
Acesta este doar unul dintre numeroasele exemple care arată cât de profund poate fi un concept aparent simplu.