Subspațiu topologic

Un subspațiu topologic este un subset al unui spațiu topologic care moștenește topologia spațiului de origine. Cu alte cuvinte, atunci când alegem o parte dintr-un spațiu topologic, putem construi o nouă topologie pe această parte, bazată pe structura inițială.

Fie \( (X, T) \) un spațiu topologic, unde \( X \) este o mulțime, iar \( T \) o colecție de mulțimi deschise care definesc topologia pe \( X \). Fie \( Y \subseteq X \). Topologia indusă pe \( Y \), numită topologia de subspațiu, se definește prin: \[ T_Y = \{ U \cap Y \mid U \in T \} \]

Altfel spus, o mulțime \( V \subseteq Y \) este deschisă în topologia subspațiului dacă există o mulțime deschisă \( U \) în \( X \) astfel încât \( V = U \cap Y \).

Toate mulțimile deschise din topologia subspațiului \( Y \) se obțin prin intersecția dintre \( Y \) și mulțimi deschise din \( X \).

$$ V_{deschis \ în \ Y} = U \cap Y $$

În mod similar, mulțimile închise din \( Y \) sunt intersecții ale lui \( Y \) cu mulțimi închise din \( X \).

$$ V_{închis \ în \ Y} = C \cap Y $$

Notă. O mulțime deschisă în \( Y \) nu este neapărat deschisă și în \( X \). Pot exista mulțimi care sunt deschise doar în subspațiu, închise doar în spațiul original sau ambele. Unele pot fi chiar simultan deschise și închise - aceste mulțimi se numesc clopen. Vom vedea imediat un exemplu concret.

Exemplu practic

Considerăm spațiul topologic \( \mathbb{R} \) cu topologia standard, în care mulțimile deschise sunt intervale deschise.

Fie \( Y = [0, 1] \) un subset al lui \( \mathbb{R} \).

Topologia indusă pe \( Y \) conține toate mulțimile de forma:

$$ U \cap [0, 1] $$

unde \( U \) este o mulțime deschisă în \( \mathbb{R} \).

De exemplu, intervalul (-1, 0.5) este deschis în \( \mathbb{R} \).

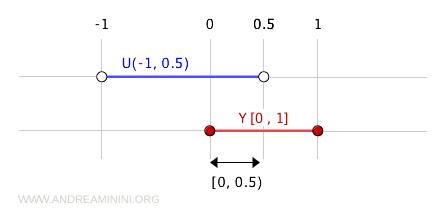
Intersecția sa cu \( Y = [0, 1] \) este:

$$ (-1, 0.5) \cap [0, 1] = [0, 0.5) $$

Rezultatul, \( [0, 0.5) \), este o mulțime deschisă în topologia subspațiului \( Y \), chiar dacă nu este deschisă în \( \mathbb{R} \).

În mod similar, intervalul \( [0, 0.5] \) este închis în topologia indusă, pentru că provine din intersecția unei mulțimi închise din \( \mathbb{R} \) cu \( Y \):

$$ [-1, 0.5] \cap [0, 1] = [0, 0.5] $$

Prin urmare, topologia indusă pe \( Y \) reflectă structura topologică a lui \( X \), dar reinterpretată în cadrul subsetului ales.

Notă. Mulțimi precum [0,a) sau (a,1], unde 0<a<1, sunt închise în \( \mathbb{R} \), dar devin deschise în topologia de subspațiu, pentru că pot fi scrise ca intersecții cu o mulțime deschisă din \( \mathbb{R} \). De exemplu: $$ (-1,0.5) \cap [0,1] = [0,0.5) $$ Astfel, [0,0.5) este deschisă în subspațiu, deși nu este deschisă în topologia standard pe \( \mathbb{R} \).

Există și mulțimi care rămân deschise și în \( \mathbb{R} \), și în \( Y \) - de exemplu (0.2, 0.8) - precum și mulțimi închise în ambele, cum este [0.2, 0.8].

În topologia subspațiului \( Y = [0, 1] \), intervalul \( [0, 1] \) este un caz interesant: este și deschis, și închis.

• Deschisă
  Alegem \( U = \mathbb{R} \), care este deschis în \( \mathbb{R} \). Intersecția sa cu \( Y \) este: $$ U \cap Y = \mathbb{R} \cap [0, 1] = [0, 1] $$ Deci \( [0, 1] \) este deschis în subspațiul \( Y \).
• Închisă
  Alegem \( C = [0, 1] \), care este închisă în \( \mathbb{R} \). $$ C \cap Y = [0, 1] \cap [0, 1] = [0, 1] $$ Prin urmare, \( [0, 1] \) este și închisă în \( Y \).

  Notă: Putem verifica și altfel: complementul lui \( [0, 1] \) în \( Y \) este mulțimea vidă, care este întotdeauna deschisă. Așadar, \( [0, 1] \) este închisă în \( Y \).

Concluzia: în topologia subspațiului \( Y = [0, 1] \), mulțimea \( [0, 1] \) este clopen, adică deschisă și închisă în același timp.

Exemplul 2

Considerăm din nou topologia standard pe mulțimea numerelor reale \( \mathbb{R} \).

Un exemplu de subspațiu interesant este mulțimea numerelor întregi \( \mathbb{Z} \). Fiecare număr întreg poate fi obținut ca intersecție între un interval deschis din \( \mathbb{R} \) și mulțimea \( \mathbb{Z} \).

De exemplu: $$ (6.5,7.5) \cap \mathbb{Z} = \{ 7 \} $$

În același mod se obțin toate celelalte numere întregi.

Astfel, fiecare număr întreg este o mulțime deschisă în topologia subspațiului \( \mathbb{Z} \). Orice subset al lui \( \mathbb{Z} \) este, la rândul său, o mulțime deschisă.

De exemplu: $$ (5.5,8.5) \cap \mathbb{Z} = \{ 6, 7, 8 \} $$

Această topologie indusă pe \( \mathbb{Z} \) se numește topologie discretă.

Notă: Topologia discretă pe \( \mathbb{Z} \) nu este o subtopologie a topologiei standard pe \( \mathbb{R} \), ci o topologie proprie. Cu toate acestea, topologia indusă pe \( \mathbb{Z} \) din \( \mathbb{R} \) coincide cu topologia discretă.

Exemplul 3

Imaginați-vă spațiul tridimensional \( \mathbb{R}^3 \), așa cum îl cunoaștem din geometrie, dar privit acum dintr-o perspectivă topologică. În topologia standard a lui \( \mathbb{R}^3 \), mulțimile deschise sunt reuniuni de bile deschise - adică regiuni din spațiu fără margini precise.

Un exemplu clasic de subspațiu al lui \( \mathbb{R}^3 \) este sfera unitară \( S^2 \), adică mulțimea tuturor punctelor aflate la distanța 1 de origine:

$$ S^2 = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 = 1 \} $$

Pe această sferă putem defini propria sa topologie, numită topologia indusă, care provine direct din cea a lui \( \mathbb{R}^3 \):

$$ T_{S^2} = \{ U \cap S^2 \mid U \text{ este deschis în } \mathbb{R}^3 \} $$

Cu alte cuvinte, o mulțime \( V \subseteq S^2 \) este deschisă pe sferă dacă poate fi obținută ca intersecția dintre sferă și o mulțime deschisă din spațiul tridimensional.

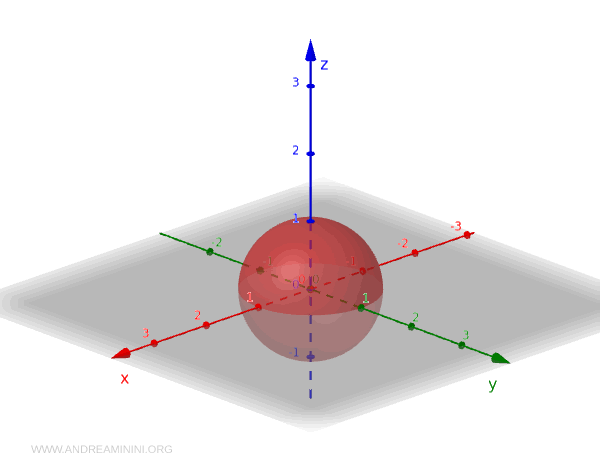
Exemple de mulțimi deschise pe sferă

• Sfera întreagă ca subspațiu deschis
  Dacă luăm mulțimea deschisă \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid x^2 + y^2 + z^2 < 2 \} \), observăm că: $$ U \cap S^2 = S^2 $$ Toate punctele sferei satisfac \( x^2 + y^2 + z^2 = 1 < 2 \), deci sfera este deschisă în propria topologie.
• Emisfera superioară
  Considerăm semispațiul superior \( U = \{ (x, y, z) \in \mathbb{R}^3 \mid z > 0 \} \). Intersecția sa cu sfera este: $$ U \cap S^2 = \{ (x, y, z) \in S^2 \mid z > 0 \} $$ Aceasta reprezintă emisfera superioară - o regiune deschisă pe sferă, pentru că este intersecția sferei cu o mulțime deschisă din \( \mathbb{R}^3 \).
• Proprietăți de bază
  Mulțimea vidă \( \emptyset \) și întreaga sferă \( S^2 \) sunt întotdeauna deschise în topologia indusă.
  
  • Intersecția finitǎ a unor mulțimi deschise în \( S^2 \) rămâne deschisă.
  • Reuniunea oricăror mulțimi deschise în \( S^2 \) este, de asemenea, deschisă.

Prin urmare, sfera \( S^2 \), privită ca subspațiu topologic al lui \( \mathbb{R}^3 \), moștenește topologia standard a spațiului tridimensional. Mulțimile deschise pe sferă sunt exact intersecțiile dintre \( S^2 \) și mulțimile deschise din \( \mathbb{R}^3 \).

Proprietățile topologiei de subspațiu

Topologia indusă are câteva reguli simple, dar esențiale:

1. Mulțimile deschise sunt toate de forma \( U \cap Y \), unde \( U \) este deschisă în spațiul original \( X \).
2. Mulțimea vidă și întreaga mulțime \( Y \) sunt întotdeauna deschise, deoarece:
   - \( \emptyset = \emptyset \cap Y \);
   - \( Y = X \cap Y \).
3. Intersecțiile finite ale mulțimilor deschise rămân deschise.
   Dacă \( V_1, \ldots, V_n \) sunt deschise în \( Y \), atunci: $$ V_1 \cap \cdots \cap V_n = (U_1 \cap \cdots \cap U_n) \cap Y $$ unde fiecare \( U_i \) este deschisă în \( X \).
4. Reuniunile arbitrare ale mulțimilor deschise sunt și ele deschise: $$ \bigcup_{\alpha \in I} V_\alpha = \left( \bigcup_{\alpha \in I} U_\alpha \right) \cap Y $$

Observații

• Topologia standard pe orice subspațiu \( Y \subseteq \mathbb{R}^n \) coincide cu topologia indusă de topologia standard pe \( \mathbb{R}^n \).
• Exemplu ilustrativ
  Fie \( Y = [-1,0) \cup (0,1] \), un subset al lui \( \mathbb{R} \). În topologia standard pe \( Y \), intervalele [-1,0) și (0,1] sunt deschise pentru că se obțin ca intersecții ale lui \( Y \) cu mulțimi deschise din \( \mathbb{R} \): $$ (-1.5,0.5) \cap Y = [-1,0) $$ $$ (0,1.5) \cap Y = (0,1] $$ Astfel, topologia standard pe \( Y \) este exact topologia indusă din \( \mathbb{R} \). În plus, aceste două intervale sunt și închise în \( Y \), deoarece complementul fiecăruia este deschis. Ele sunt, așadar, mulțimi clopen - deschise și închise simultan.
• Teorema bazei pentru topologia indusă
  Dacă \( B_X \) este o bază pentru topologia unui spațiu \( X \) și \( Y \subset X \), atunci colecția: $$ B_Y = \{ B \cap Y \mid B \in B_X \} $$ constituie o bază pentru topologia indusă pe \( Y \).

Topologia de subspațiu este una dintre ideile fundamentale ale topologiei generale. Ea arată cum putem privi o parte a unui spațiu topologic păstrând structura sa internă - o idee cheie pentru analiza geometrică, teoria varietăților și studiul spațiilor continue.