Mulțimi care nu sunt nici deschise, nici închise

În topologie, există mulțimi care nu pot fi încadrate nici în categoria mulțimilor deschise, nici în cea a mulțimilor închise, deoarece nu îndeplinesc cerințele necesare pentru niciuna dintre ele.

Acest tip de situație apare în topologii unde o mulțime nu este recunoscută ca mulțime deschisă și, în același timp, nici ca fiind complementara unei mulțimi deschise. În asemenea cazuri, clasificarea obișnuită devine insuficientă, iar mulțimea rămâne într-o zonă intermediară.

Prin urmare, o astfel de mulțime nu poate fi considerată nici mulțime închisă. Chiar dacă în topologia numerelor reale asemănarea poate părea nefirească, în topologii mai generale aceste exemple sunt frecvente și perfect logice. O situație concretă poate ajuta la înțelegerea ideii.

Exemplu explicat pas cu pas

Considerăm mulțimea \( X = \{a,b,c,d\} \) și o topologie \( T \) compusă din următoarele mulțimi deschise: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) și mulțimea vidă (Ø).

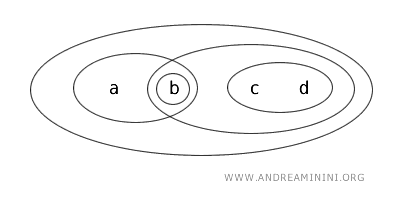
Ne concentrăm asupra submulțimii \( \{b,c\} \). Observăm următoarele:

• Submulțimea \( \{b,c\} \) nu este deschisă, deoarece nu apare în lista mulțimilor deschise definite în topologia \( T \).
• În același timp, \( \{b,c\} \) nu este nici închisă, fiindcă mulțimea complementară \( X \setminus \{b,c\} = \{a,d\} \) nu aparține colecției mulțimilor deschise din \( T \).

Rezultatul este clar: în topologia \( T \), mulțimea \( \{b,c\} \) nu poate fi clasificată drept mulțime deschisă sau mulțime închisă. Situații similare apar frecvent în diverse structuri topologice, unde intuiția trebuie completată cu rigoare formală.