Topologia mulțimilor deschise
O topologie T definită pe o mulțime X este o colecție de submulțimi ale acesteia, numite „mulțimi deschise", care îndeplinesc câteva condiții simple, dar esențiale pentru studierea structurii spațiului.
- Mulțimea vidă Ø și mulțimea întreagă X sunt considerate deschise prin definiție.
- Uniunea oricăror mulțimi deschise și intersecția unui număr finit de astfel de mulțimi sunt, la rândul lor, mulțimi deschise.
Cu alte cuvinte, topologia T reunește toate submulțimile lui X declarate „deschise", iar această colecție trebuie să rămână stabilă atunci când aplicăm operațiile de uniune sau intersecție.
O colecție de mulțimi este o mulțime ale cărei elemente sunt ele însele submulțimi. Aceasta este ideea de bază din spatele unei topologii.
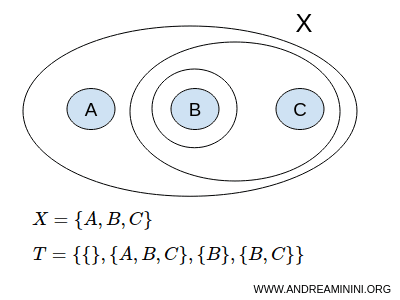
Împreună, mulțimea X și topologia T formează un spațiu topologic, notat în mod obișnuit prin perechea (X,T).
Notă: În vorbirea curentă se spune adesea că „X este un spațiu topologic". De fapt, un spațiu topologic este alcătuit atât din mulțimea X, cât și din colecția T a mulțimilor deschise.
De ce este mulțimea vidă considerată mereu deschisă?
Mulțimea vidă apare automat ca mulțime deschisă în orice spațiu topologic. Această convenție asigură coerența definițiilor și permite funcționarea corectă a întregii teorii.
Exemplu concret
Să luăm mulțimea X formată din trei elemente: A, B și C.
$$ X = \{ A,B,C \} $$
Presupunem acum că topologia T este formată din următoarele submulțimi: { }, {A,B,C}, {B}, {B,C}.
$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \} \} $$
Aici, { } reprezintă mulțimea vidă Ø, iar {A,B,C} este mulțimea completă. Acestea sunt numite submulțimi improprii.
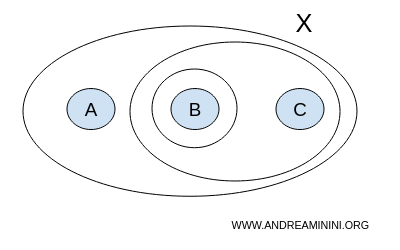
Observăm că această colecție respectă regulile topologiei. Uniunile dintre mulțimile sale rămân în T. De exemplu:
$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$
$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$
$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$
$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$
La fel se întâmplă și cu intersecțiile:
$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$
$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$
$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$
Rezultă clar că T este într-adevăr o topologie pe mulțimea X.
Exemplul 2
Păstrăm aceeași mulțime X, dar schimbăm colecția T:
$$ X = \{ A,B,C \} $$
De data aceasta, T conține și submulțimea {A}:
$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \} \} $$
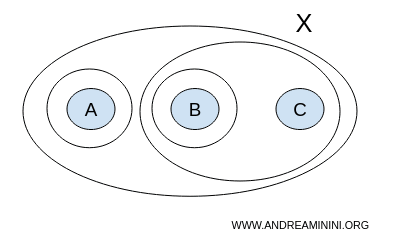
Deși pare asemănătoare cu exemplul anterior, această colecție nu este o topologie. De exemplu, uniunea submulțimilor {A} și {B} produce mulțimea {A,B}, care nu se află în T:
$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\notin} T $$
Această încălcare este suficientă pentru a respinge colecția ca topologie, deoarece operația de uniune nu mai păstrează mulțimile în interiorul lui T.
Prin urmare, această colecție T nu definește o topologie pe mulțimea X.
Și așa mai departe