Colecții de mulțimi

O colecție de mulțimi este o mulțime ale cărei elemente sunt, la rândul lor, mulțimi.

Cu alte cuvinte, este o mulțime constituită exclusiv din mulțimi.

Această noțiune este prezentă în numeroase ramuri ale matematicii, în special în teoria mulțimilor, topologie și algebră abstractă.

Care este utilitatea ? O colecție de mulțimi face posibilă construirea unor structuri matematice mai sofisticate și analiza relațiilor dintre diferite mulțimi.

Iată câteva exemple reprezentative de colecții de mulțimi :

• Familie de mulțimi
  O colecție de mulțimi care împărtășesc o proprietate comună sau satisfac anumite criterii prestabilite. Un exemplu clasic este familia tuturor mulțimilor deschise dintr-un spațiu topologic.
• Partiția unei mulțimi
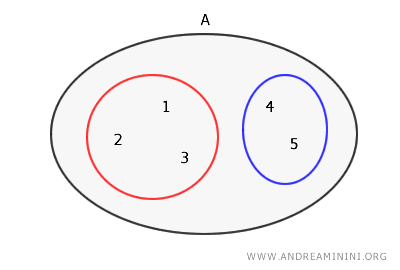
  O partiție este o colecție de submulțimi disjuncte a căror reuniune reconstituie exact mulțimea inițială. Altfel spus, fiecare element aparține unei singure submulțimi din partiție.

  De exemplu, dacă luăm mulțimea A = {1, 2, 3, 4, 5}, o posibilă partiție a lui A este colecția formată din submulțimile { {1, 2, 3}, {4, 5} }.
  

• Mulțimea părților (mulțimea tuturor submulțimilor)
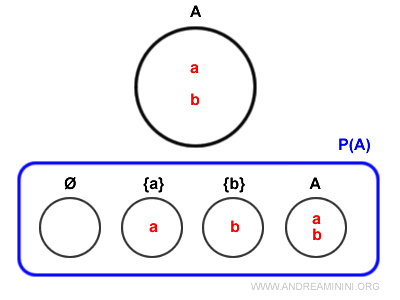
  Aceasta este colecția alcătuită din toate submulțimile posibile ale unei mulțimi date, incluzând atât mulțimea vidă, cât și mulțimea însăși.

  De exemplu, pentru mulțimea A = {a, b}, mulțimea părților P(A) este compusă din următoarele submulțimi : { {}, {a}, {b}, {a, b} }.
  

Astfel de concepte joacă un rol fundamental în studiul structurilor matematice avansate și permit investigarea în profunzime a relațiilor și proprietăților mulțimilor în diverse cadre teoretice.