Produsul Cartezien

Produsul cartezien este o operație fundamentală în matematică, definită între două mulțimi.

Definiție

Fie două mulțimi A și B. Produsul cartezien A×B este mulțimea formată din toate perechile ordonate (a,b), unde primul element „a” aparține mulțimii A, iar al doilea element „b” aparține mulțimii B.

În limbaj matematic, produsul cartezien se scrie astfel:

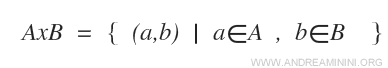
Se citește „A înmulțit cu B” sau „A cartezien B”.

Un Exemplu Practic

Pentru a înțelege mai clar ce înseamnă produsul cartezien, să analizăm un exemplu concret.

Să presupunem că avem două mulțimi A și B: prima conține două elemente, iar a doua trei elemente.

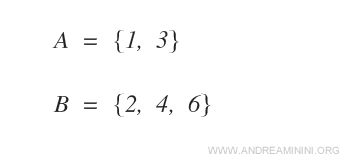
Produsul cartezien A×B este următoarea mulțime:

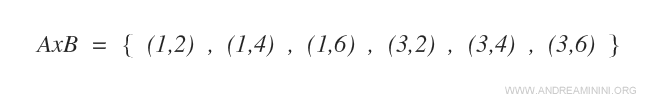
Fiecare element al produsului cartezien A×B este o pereche ordonată.

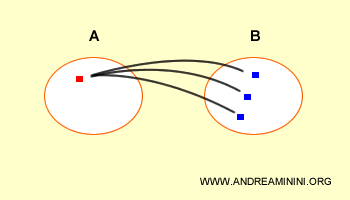
Grafic, relația dintre cele două mulțimi poate fi reprezentată astfel:

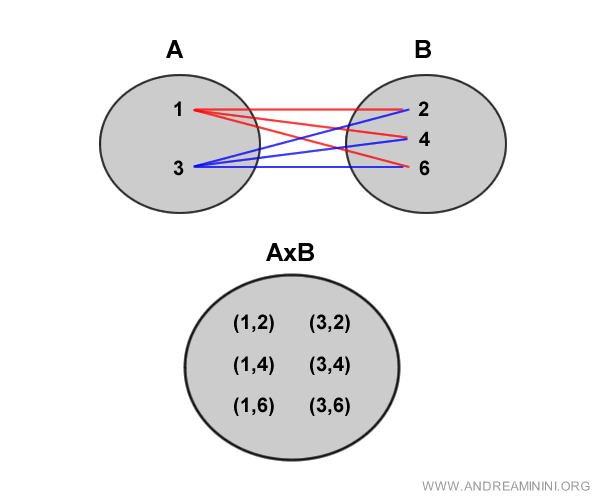
Notă. Elementele produsului cartezien nu aparțin separat mulțimii A sau B, ci alcătuiesc o nouă structură: perechi ordonate ce combină elemente din ambele mulțimi.

Într-un sistem de coordonate cartezian, aceste perechi pot fi reprezentate ca puncte (x,y).

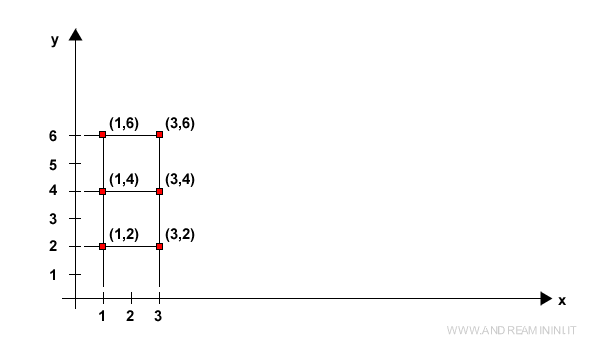
Cum se Reprezintă Produsul Cartezien?

Produsul cartezien poate fi ilustrat în mai multe moduri:

• Prin diagramă carteziană
  Într-un sistem de coordonate, elementele mulțimii A se așază pe axa x (orizontală), iar cele ale mulțimii B pe axa y (verticală). Fiecare pereche ordonată (a,b) corespunde unui punct unic din planul cartezian, cu coordonatele (x=a, y=b).
  
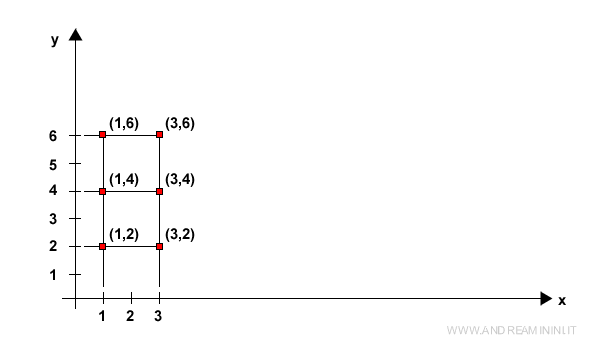
• Prin tabel cu dublă intrare
  Într-un tabel, elementele mulțimii A se notează pe rânduri, iar elementele mulțimii B pe coloane. În fiecare celulă apare perechea ordonată corespunzătoare intersecției dintre rând și coloană.
  

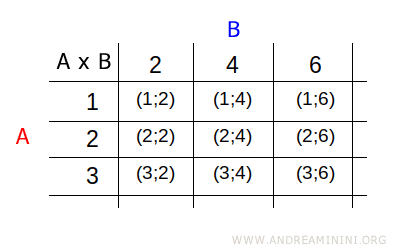
  Notă. Această reprezentare este foarte utilă atunci când mulțimile conțin elemente care nu sunt numere.

Ce este o Pereche Ordonată?

O pereche ordonată (a,b) este un cuplu de elemente în care ordinea este esențială: primul element este „a”, iar al doilea este „b”.

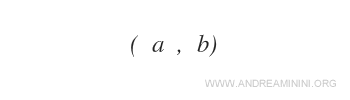
Perechile ordonate se scriu între paranteze și elementele sunt separate prin virgulă.

Este posibil ca cele două elemente să fie identice.

Ordinea contează

Ordinea elementelor într-o pereche nu poate fi inversată.

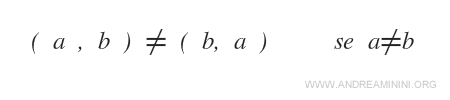
Exemplu

Perechile (2,4) și (4,2) sunt diferite: deși conțin aceleași numere, schimbarea ordinii le modifică semnificația.

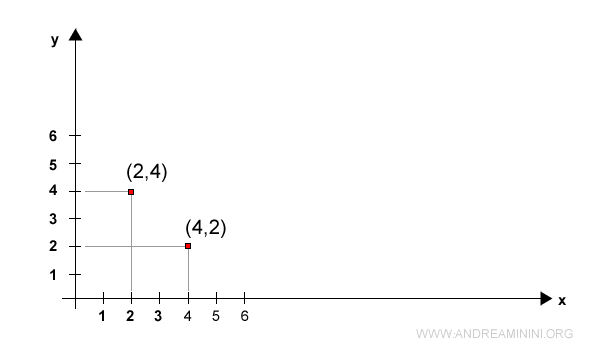
Când sunt două perechi ordonate egale?

Două perechi (a,b) și (c,d) sunt egale dacă și numai dacă elementele lor coincid în aceeași ordine, adică a=c și b=d.

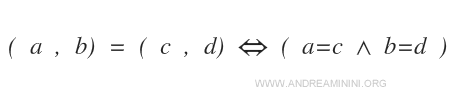
Proprietatea Comutativă a Produsului Cartezien

Produsul cartezien nu este comutativ.

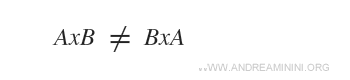
Exemplu

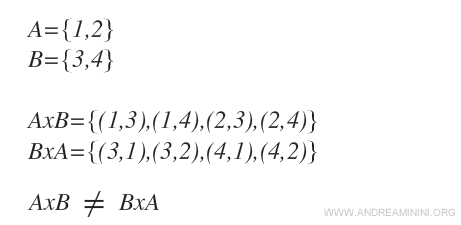
Este clar că A×B ≠ B×A, deoarece, spre deosebire de o mulțime, într-o pereche ordonată ordinea elementelor are importanță.

Această diferență devine evidentă atunci când reprezentăm cele două produse carteziene într-un plan cartezian.

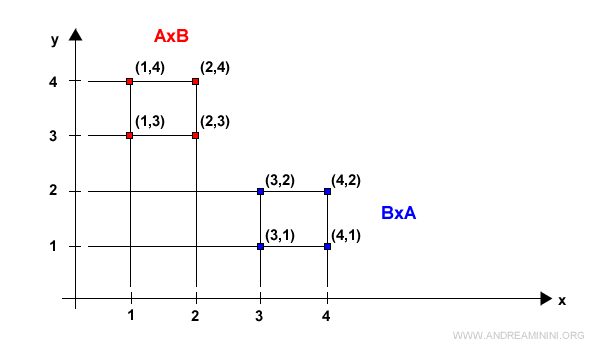
Notă. Singurul caz în care A×B = B×A apare atunci când A = B. Dacă cele două mulțimi coincid, produsul cartezien respectă proprietatea comutativă.

Proprietatea Distributivă

Produsul cartezien respectă proprietatea distributivă față de reuniunea și intersecția mulțimilor.

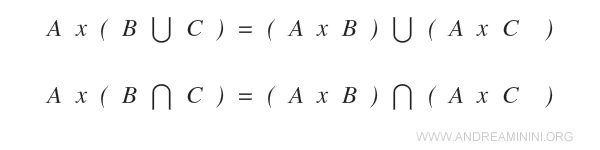
Demonstrație

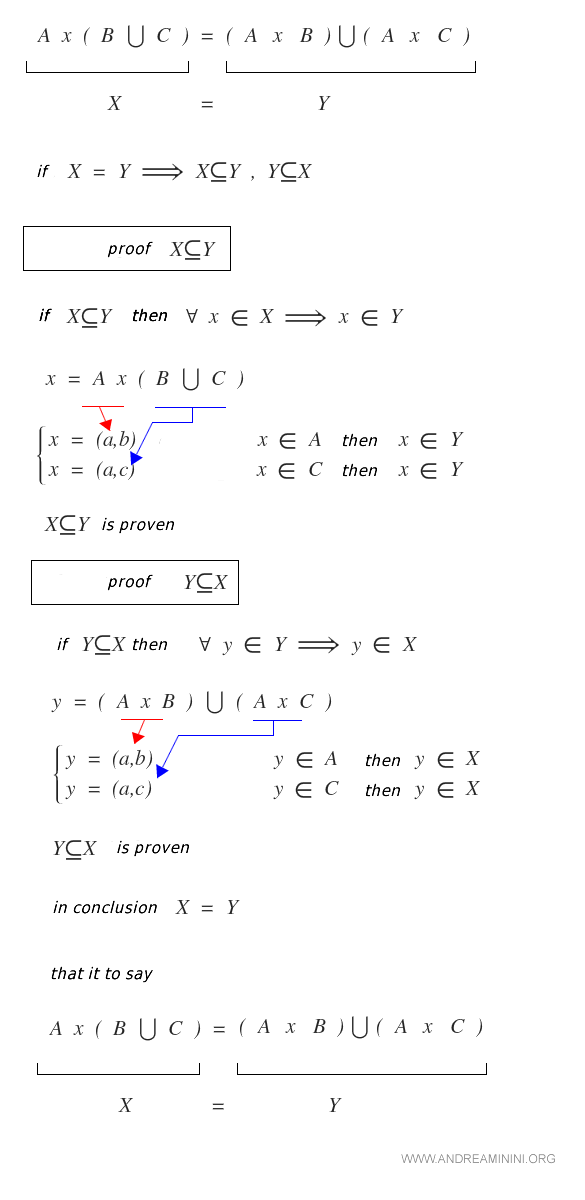
Produsul Cartezien cu Mulțimea Vidă

Dacă una dintre mulțimi este vidă, produsul cartezien este de asemenea o mulțime vidă.

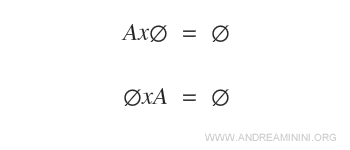
Produsul Cartezien al n Mulțimi

Produsul cartezien nu se limitează la două mulțimi, ci poate fi extins la un număr arbitrar n de mulțimi.

Date n mulțimi A₁, A₂,..., A_n, produsul cartezien A₁×A₂×...×A_n este mulțimea tuturor n-tuplurilor (a₁, a₂,..., a_n): $$ A_1\:x\:A_2\:x\:...\:x\:A_n = \{ (a_1,a_2,...,a_n) | a_i \in A_i , i=1,2,...,n \} $$

Fiecare element a_i aparține mulțimii A_i corespunzătoare.

Produsul Cartezien al unei Mulțimi cu Ea Însăși

Putem calcula și produsul cartezien al unei mulțimi cu ea însăși.

Exemplu

Să considerăm mulțimea A:

$$ A = \{ 1,2,3 \} $$

Produsul cartezien al lui A cu ea însăși, A×A, este mulțimea perechilor ordonate:

$$ A×A = \{ (1,1) , (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) \} $$

Acest concept se poate extinde la produse carteziene de dimensiuni superioare, obținând triple, cvadruple sau, în general, n-tupluri.