Submulțimi

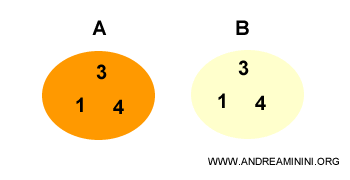
Spunem că o mulțime A este submulțime a lui B dacă fiecare element al lui A se găsește și în B.

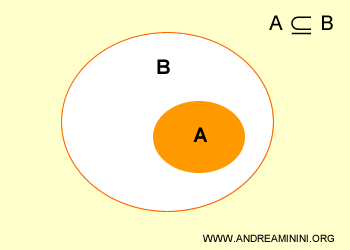
Reprezentarea grafică a mulțimilor de mai sus poartă numele de diagramă Venn.

Cu alte cuvinte, submulțimea A este inclusă în mulțimea B.

Această relație se numește incluziune.

Pentru a nota incluziunea obișnuită, se folosește simbolul ⊆.

Se citește: „mulțimea A este inclusă în mulțimea B”.

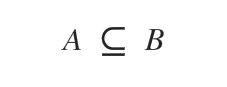
Această notație se mai poate interpreta și ca „A este o submulțime a lui B” sau „A este conținută în B”.

Relația de incluziune poate fi exprimată și astfel:

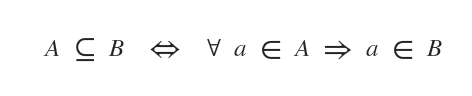
Notă. Relația de incluziune acoperă și cazul în care A și B sunt mulțimi identice, adică au exact aceleași elemente. De fapt, simbolul este format din simbolul de incluziune (⊂) și cel de egalitate (=).

Submulțimea proprie

O submulțime proprie este o mulțime A inclusă în B, dar pentru care există cel puțin un element în B care nu aparține lui A.

Pe scurt, mulțimile sunt diferite, adică A≠B.

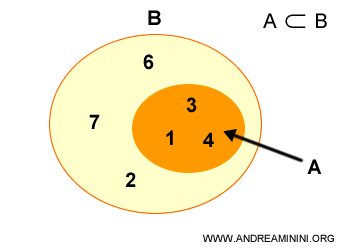
Această situație poartă numele de incluziune strictă.

Este un caz particular de incluziune, reprezentat prin simbolul ⊂.

Înseamnă: „mulțimea A este o parte proprie a lui B”.

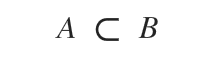
Se poate exprima și astfel: „mulțimea A este inclusă strict în mulțimea B”.

Exemplu

Mulțimea A este inclusă strict în mulțimea B:

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4,2,6,7 \} $$

Toate elementele lui A se regăsesc în B, dar B are elemente care lipsesc din A.

$$ A ⊂ B $$

Diferența dintre incluziunea obișnuită și cea strictă: În incluziunea strictă (A⊂B), mulțimile A și B sunt întotdeauna diferite (A≠B). În incluziunea obișnuită (A⊆B), cele două mulțimi pot fi și identice (A=B). Prin urmare, dacă A⊂B este adevărat, atunci și A⊆B este adevărat. $$ A⊂B \Longrightarrow A⊆B $$ În schimb, dacă A⊆B este adevărat, nu rezultă neapărat că A⊂B este adevărat, deoarece mulțimile ar putea fi identice.

Submulțimea improprie

A] Mulțimea identică cu ea însăși

Când A = B, fiecare este submulțime a celeilalte.

În acest caz, spunem că:

• A este o submulțime improprie a lui B
• B este o submulțime improprie a lui A

Această incluziune reciprocă implică egalitatea mulțimilor.

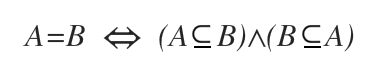
Așadar, când două mulțimi sunt egale, ele sunt și submulțimi improprii una a celeilalte.

Exemplu

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4 \} $$

Fiecare element din A se regăsește în B și invers, deci A = B.

B] Mulțimea vidă

Mulțimea vidă este considerată submulțime improprie a oricărei mulțimi.

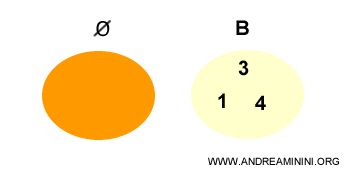
Este definită ca mulțimea fără elemente.

Se notează cu Ø. $$ Ø = \{ \ \ \} $$

Notă: Faptul că mulțimea vidă este submulțime a tuturor mulțimilor poate părea inițial paradoxal, dar se demonstrează riguros (vezi demonstrația).

Exemplu

$$ Ø = \{ \ \ \} $$

$$ A = \{ 1,3,4 \} $$

Mulțimea vidă este inclusă strict în A:

$$ Ø ⊂ A $$

Demonstrație: Prin reducere la absurd, presupunem contrariul. Dacă Ø nu ar fi submulțime a lui A, ar exista un element în Ø care nu aparține lui A. Dar Ø nu conține niciun element, deci presupunerea e falsă, iar afirmația opusă este adevărată. Demonstrație alternativă: Reuniunea unei mulțimi A cu o submulțime B⊆A este întotdeauna A. $$ A \cup B = A $$ La fel, reuniunea cu mulțimea vidă nu schimbă mulțimea: $$ A \cup Ø = A $$

Singleton-ul

Ce este un singleton?

Un singleton este o submulțime cu un singur element.

Exemplu

Mulțimea B este un singleton deoarece B⊂A și conține un singur element.

$$ A = \{ 1, 2, 3, 4, 5\} $$

$$ B = \{ 2 \} $$

Diferența dintre incluziune și apartenență

Este important să nu confundăm aceste două noțiuni:

• Incluziunea ⊆ se folosește exclusiv între mulțimi și indică faptul că A este submulțime a lui B. $$ A \subseteq B $$
• Apartenența ∈ se folosește între elemente și o mulțime și arată că un element, de exemplu a, aparține mulțimii A. $$ a \in A $$

Notă: Același principiu se aplică și neincluziunii și neapartenenței: $$ a \notin A \\ A \nsubseteq B $$