Mulțime parțial ordonată

O mulțime înzestrată cu o relație de ordine parțială se numește mulțime parțial ordonată, sau, pe scurt, poset. Aceasta se notează prin (A, ≤).

Ce înțelegem prin ordine parțială?

Dată o mulțime A, o ordine parțială este o relație

$$ ≤:A \times A \rightarrow \{ \text{adevărat}, \text{fals} \}. $$

Cu alte cuvinte, pentru orice pereche (x, y) din A putem decide dacă se verifică sau nu relația de ordine ≤.

Un exemplu concret

Să considerăm o mulțime finită A cu șapte elemente:

$$ A = \{ a, b, c, d, e, f \} $$

Definim o relație ≤ pe produsul cartezian A × A:

$$ ≤ = \{ (a,c), (a,e), (b,d), (b,f), (c,g), (d,g), (e,g), (f,g) \} $$

Perechea (A, ≤) constituie un poset.

Observație. Relația nu este definită pentru toate perechile de elemente din mulțime. De exemplu, nu există relație între (a, b), (a, d) ș.a.m.d.

Relațiile din posetul (A, ≤) pot fi reprezentate prin următorul graf:

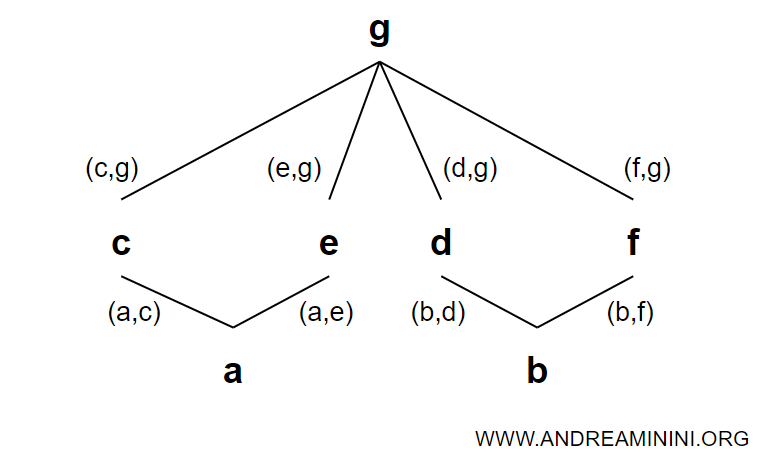
Fiecare săgeată indică o relație de ordine între elementele pe care le unește.

Alte exemple de poseturi

• Numerele naturale
  Mulțimea \( (\mathbb{N}, \leq) \) a numerelor naturale, cu ordinea obișnuită „mai mic sau egal”, este un poset. Relația are proprietățile de reflexivitate, antisimetricitate și tranzitivitate.

  De exemplu, pentru două elemente arbitrare din \( \mathbb{N} = \{0, 1, 2, 3, \dots\} \), se poate stabili întotdeauna care dintre ele este mai mic sau egal cu celălalt.

• Mulțimea putere ordonată prin incluziune
  Dacă \( S \) este o mulțime, mulțimea putere \( \mathcal{P}(S) \) - adică mulțimea tuturor submulțimilor sale - formează un poset în raport cu relația de incluziune (\(\subseteq\)). Aici, ordinea este dată de relația de incluziune, și nu de valori numerice.

  De pildă, dacă \( S = \{a, b\} \), atunci \( \mathcal{P}(S) = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} \). Mulțimea vidă Ø este inclusă în toate celelalte, iar {a} și {b} sunt incluse în {a, b}. În schimb, {a, b} nu este inclusă nici în {a}, nici în {b}. $$ \emptyset \subseteq \{ a \} \\ \{ a \} \subseteq \{a, b\} \\ \{ b \} \subseteq \{a, b\} \\ \vdots $$ Aceste relații de incluziune se pot ilustra printr-o diagramă de rețea, unde fiecare nod corespunde unui subansamblu, iar muchiile indică incluziunea, orientată de jos în sus.
  

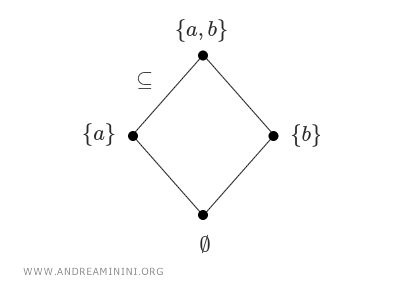
• Divizibilitatea în numerele întregi
  Un alt exemplu clasic de poset este mulțimea numerelor întregi \( \mathbb{Z} \), ordonată prin relația de divizibilitate. Spunem că \( x \mid y \) dacă x îl divide pe y, ceea ce definește o ordine parțială pe anumite submulțimi de întregi.

  De exemplu, 4 divide 8 (4 | 8), deci relația este adevărată; în schimb, 6 nu divide 8, deci 6 | 8 este fals. Considerăm mulțimea S = {2, 4, 6, 8, 12, 24} sub această relație. Diagrama lui Hasse asociată reprezintă fiecare număr ca nod, iar muchiile (sau lanțuri de muchii) leagă divizorii de multiplii lor, orientate de jos în sus.
  
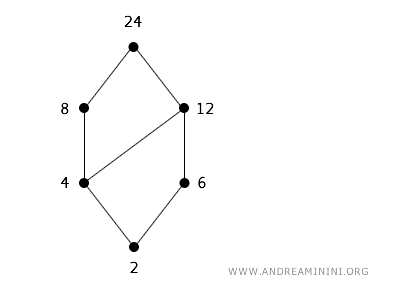
  În acest caz, 2 divide toate celelalte elemente: 4, 6, 8, 12 și 24. Reciprocul nu este valabil: de exemplu, 6 divide 12 și 24, dar nu divide 2, 4 sau 8.

Proprietăți fundamentale ale unui poset

Un poset este o pereche (S, ≤) unde S este o mulțime, iar ≤ o relație binară care respectă următoarele proprietăți:

• Reflexivitate: Fiecare element se raportează la sine însuși: $$ \forall x \in S,\ x \le x $$
• Antisimetricitate: Dacă două elemente se raportează reciproc, atunci ele sunt identice: $$ \forall x, y \in S,\ (x \le y \land y \le x) \Rightarrow x = y $$
• Tranzitivitate: Dacă x ≤ y și y ≤ z, atunci x ≤ z: $$ \forall x, y, z \in S,\ (x \le y \land y \le z) \Rightarrow x \le z $$

În concluzie, un poset este o mulțime împreună cu o relație reflexivă, antisimetrică și tranzitivă, dar care nu este neapărat totală. Cu alte cuvinte, nu orice pereche de elemente ale mulțimii trebuie să fie comparabilă între ele.

Poseturile constituie o noțiune fundamentală în teoria rețelelor și apar în aplicații importante, de pildă în algebra comutativă (mulțimea idealurilor unui inel) și în topologia algebrică.

Infim și suprem

Fie un poset (A, ≤) și un subansamblu B al lui A:

• Infimul lui B, notat inf(B), este cel mai mare element din A care este mai mic sau egal cu toate elementele din B.
• Supremul lui B, notat sup(B), este cel mai mic element din A care este mai mare sau egal cu toate elementele din B.

Exemplu

Subansamblul B are infimul 3 și supremul 4.

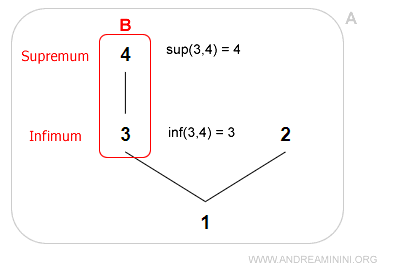
Observație. Un subansamblu nu posedă întotdeauna un infim sau un suprem; însă atunci când ele există, sunt determinate în mod unic.

Cote inferioare și superioare

Fie (A, ≤) un poset și B un subansamblu al lui A:

• Un element \( k \in A \) este o cotă inferioară a lui B dacă \( k \le b \) pentru orice \( b \in B \).

  Exemplu. Dacă A = {1, 2, 3, 4, 5, 6} și B = {3, 4}, atunci mulțimea cotelor inferioare ale lui B este {1, 2, 3}.

• Un element \( k \in A \) este o cotă superioară a lui B dacă \( k \ge b \) pentru orice \( b \in B \).

  Exemplu. Pentru aceleași A și B, mulțimea cotelor superioare ale lui B este {4, 5, 6}.

Elemente maxime și minime

Într-un poset (A, ≤):

• Un element minim este un element care nu are niciun predecesor în A.

  Exemplu. În A = {1, 2, 3, 4, 5, 6}, elementul minim este 1.

• Un element maxim este un element care nu are niciun succesor în A.

  Exemplu. În aceeași mulțime, elementul maxim este 6.

Un poset poate conține mai multe elemente maxime sau minime.

Exemplu

Diagrama de mai jos prezintă trei elemente maxime și unul minim.

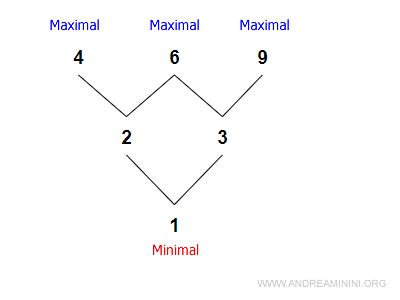
Relația de ordine este:

$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$

Rezultă că:

• 4, 6 și 9 nu au succesori în mulțime: sunt elemente maxime.
• 1 nu are predecesori: este elementul minim.

Observație. În poseturile infinite nu există neapărat elemente maxime sau minime. În schimb, orice poset finit are cel puțin unul de fiecare tip.

Maxim și minim

Într-un poset (A, ≤):

• Minimul este elementul unic care este mai mic sau egal cu toate celelalte elemente din A.
• Maximul este elementul unic care este mai mare sau egal cu toate celelalte elemente din A.

Nu toate poseturile admit un minim sau un maxim.

Exemplu

În următorul caz, 1 este minimul, însă nu există un maxim.

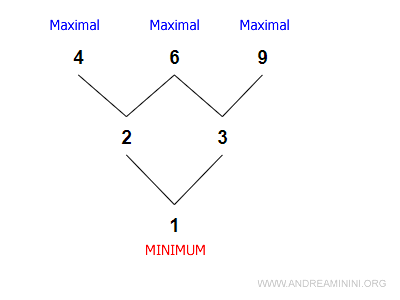
Relația de ordine este:

$$ ≤ = \{ (1,2), (1,3), (2,4), (2,6), (3,6), (3,9) \} $$

Se poate verifica faptul că 1 este minimul, deoarece:

$$ 1 \leq 2 \\ 1 \leq 3 \\ 1 \leq 4 \\ 1 \leq 6 \\ 1 \leq 9 $$

Totuși, nu putem afirma că 9 este maximul, întrucât nu știm dacă relațiile (2,9), (4,9) și (6,9) sunt satisfăcute:

$$ 1 \leq 9 \\ 3 \leq 9 \\ 2 \; ? \; 9 \\ 4 \; ? \; 9 \\ 6 \; ? \; 9 $$

Aceeași incertitudine apare și pentru ceilalți candidați la maxim:

4 nu poate fi maxim, deoarece nu știm dacă (4,9), (4,6) sau (4,3) se verifică:

$$ 1 \leq 4 \\ 2 \leq 4 \\ 4 \; ? \; 3 \\ 4 \; ? \; 6 \\ 4 \; ? \; 9 $$

6 de asemenea nu este maxim, pentru că nu știm dacă (6,4) sau (6,9) sunt adevărate:

$$ 1 \leq 6 \\ 2 \leq 6 \\ 3 \leq 6 \\ 4 \; ? \; 6 \\ 9 \; ? \; 6 $$

Și așa mai departe.