Diferența Simetrică dintre Mulțimi

Diferența simetrică a două mulțimi A și B este mulțimea elementelor care aparțin uneia dintre ele, dar nu se regăsesc simultan în ambele. Ea se notează astfel: $$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Această operație evidențiază elementele specifice fiecărei mulțimi, eliminându-le pe cele comune.

Definiția formală este următoarea:

$$ A \Delta B = (A \setminus B) \cup (B \setminus A) $$

Unde:

• A\B reprezintă mulțimea elementelor aflate în A, dar nu în B.
• B\A reprezintă mulțimea elementelor aflate în B, dar nu în A.

Cu alte cuvinte, diferența simetrică este reuniunea elementelor care aparțin exclusiv fiecărei mulțimi.

Această operație este utilă mai ales atunci când dorim să subliniem diferențele dintre două mulțimi.

Într-o diagramă Venn, diferența simetrică este reprezentată prin regiunile care nu se suprapun între cele două cercuri ce simbolizează mulțimile.

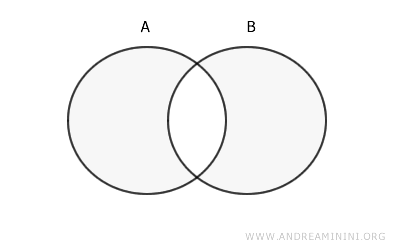
Un Exemplu Practic

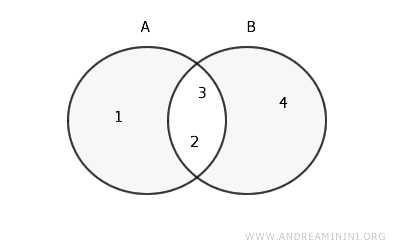
Să considerăm următoarele mulțimi A și B:

$$ A = \{1, 2, 3\} $$

$$ B = \{2, 3, 4\} $$

Pentru a determina diferența simetrică \(A \Delta B\), identificăm elementele care se află în A dar nu în B și, respectiv, cele care se află în B dar nu în A:

$$ A \setminus B = \{1\} $$

$$ B \setminus A = \{4\} $$

Rezultă că diferența simetrică dintre A și B este mulțimea {1, 4}.

$$ A \Delta B = \{1\} \cup \{4\} = \{1, 4\} $$

Grafic, într-o diagramă Venn, situația ar arăta astfel:

Exemplul 2

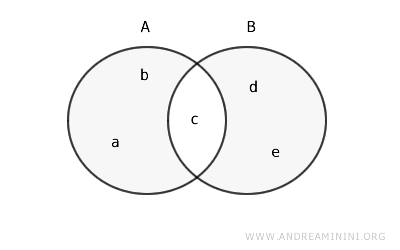
Să analizăm un alt caz:

$$ A = \{a, b, c\} $$

$$ B = \{c, d, e\} $$

Aplicând același raționament, obținem:

$$ A \setminus B = \{a, b\} $$

$$ B \setminus A = \{d, e\} $$

Așadar, diferența simetrică dintre A și B este mulțimea {a, b, d, e}.

$$ A \Delta B = \{a, b\} \cup \{d, e\} = \{a, b, d, e\} $$

Într-o diagramă Venn, ea se reprezintă astfel:

Proprietățile Diferenței Simetrice

Diferența simetrică are câteva proprietăți importante:

• Comutativitate
  Ordinea mulțimilor nu influențează rezultatul: \[ A \Delta B = B \Delta A \]
• Asociativitate
  Gruparea diferită a mulțimilor nu modifică rezultatul: \[ A \Delta (B \Delta C) = (A \Delta B) \Delta C \]
• Element neutru
  Diferența simetrică dintre o mulțime și mulțimea vidă este chiar mulțimea inițială: \[ A \Delta \emptyset = A \]
• Idempotentă
  Diferența simetrică dintre o mulțime și ea însăși este mulțimea vidă: \[ A \Delta A = \emptyset \]

Aceste proprietăți fac din diferența simetrică un concept esențial și foarte util în diverse contexte matematice.