Diferența dintre Mulțimi
Diferența dintre două mulțimi A și B este o mulțime (numită mulțimea diferență) formată din elementele lui A care nu aparțin lui B: $$ A-B = \{ x \ | \ x \in A \ ∧ \ x \notin B \} $$. Se citește „A minus B”. Mai jos este prezentată diagrama Venn corespunzătoare.
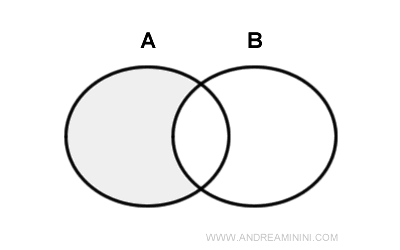
În anumite situații, diferența dintre mulțimi se notează și astfel:
$$ A \text{ \ } B $$
Se interpretează ca „mulțimea A\B este complementul mulțimii B”.
Exemplu practic
Să presupunem că avem două mulțimi finite A și B:
$$ A = \{ 0, 2, 4, 8, 10 \} $$
$$ B = \{ 2, 4, 6, 12 \} $$
Diferența A-B conține elementele lui A care nu se regăsesc în B:
$$ A-B = A \text{ \ } B = \{ 0, 8, 10 \} $$
Mulțimea diferență este alcătuită din elementele lui A care nu apar în B, adică { 0, 8, 10 }.
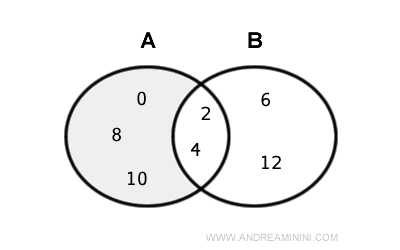
Elementele comune celor două mulțimi (în acest caz 2 și 4) sunt eliminate din mulțimea diferență.
Exemplul 2
Să analizăm un alt caz, cu următoarele mulțimi finite:
$$ A = \{ 1, 2, 3, 4, 5, 6, 7 \} $$
$$ B = \{ 2, 4, 6 \} $$
Aici, mulțimea B este un subansamblu propriu al lui A.
Diferența A-B este mulțimea elementelor lui A care nu se află în B:
$$ A-B = A \text{ \ } B = \{ 1, 3, 5, 7 \} $$
Mulțimea diferență este, așadar, { 1, 3, 5, 7 }.
În diagramele Euler - Venn, diferența este evidențiată în gri.
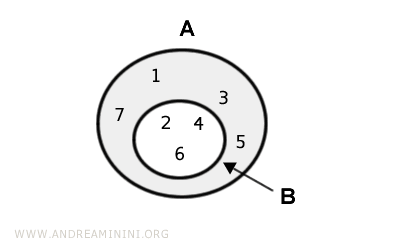
Proprietăți ale diferenței
Câteva proprietăți importante ale diferenței dintre mulțimi:
- Diferența dintre mulțimi nu este comutativă $$ A-B \ne B-A $$
Exemplu. Pentru $$ A = \{ 0, 2, 4, 8, 10 \} $$ și $$ B = \{ 2, 4, 6, 12 \} $$ avem: $$ A-B = \{ 0, 8, 10 \} $$ iar $$ B-A = \{ 6, 12 \} $$
- Dacă mulțimile sunt disjuncte, diferența A-B este egală cu A $$ A \cap B = Ø \Longleftrightarrow A-B = A $$
Exemplu. Pentru $$ A = \{ 2, 4, 6, 8 \} $$ și $$ B = \{ 1, 3, 5, 7, 9 \} $$ rezultă: $$ A-B = A = \{ 2, 4, 6, 8 \} $$. Reprezentarea grafică:
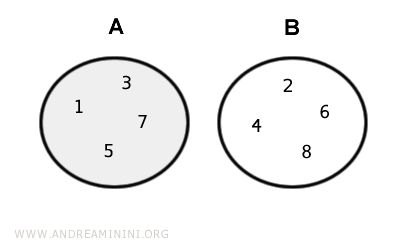
Similar, $$ B-A = B = \{ 1, 3, 5, 7, 9 \} $$ - Dacă mulțimile sunt egale, diferența A-B este mulțimea vidă $$ A = B \Longleftrightarrow A-B = Ø $$
Aceste proprietăți se aplică oricăror mulțimi în operațiile de diferență.