Diferența dintre mulțimile deschise și cele închise

Noțiunile de mulțimi deschise și mulțimi închise sunt fundamentale pentru înțelegerea structurii spațiilor topologice. Diferența esențială dintre ele constă în includerea sau excluderea punctelor de frontieră din cadrul mulțimii.

O mulțime închisă conține toate punctele sale de frontieră, în timp ce o mulțime deschisă le exclude.

Cu alte cuvinte, punctele de frontieră aparțin unei mulțimi închise, dar sunt exterioare unei mulțimi deschise.

Să examinăm mai atent aceste două concepte :

• Mulțime deschisă

  O mulțime deschisă este o mulțime care nu conține niciunul dintre punctele sale de frontieră.

  Mai riguros, o mulțime \(A\) dintr-un spațiu topologic \(X\) se numește deschisă dacă, pentru fiecare punct \(x \in A\), există un vecinaj complet conținut în \(A\). Cu alte cuvinte, în jurul fiecărui punct al mulțimii se poate trasa un „vecinaj” care rămâne integral în interiorul acesteia, fără a intersecta frontiera.
  

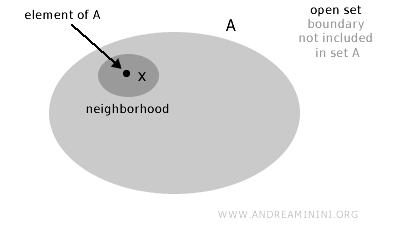
  Exemplu. Un exemplu simplu de mulțime deschisă este intervalul \( (3,10) \) din mulțimea numerelor reale. Acesta conține toate numerele \( x \) pentru care \( 3 < x < 10 \), dar exclude capetele 3 și 10. Deoarece aceste valori nu aparțin intervalului, exemplul ilustrează perfect noțiunea de mulțime deschisă într-un context unidimensional.
  

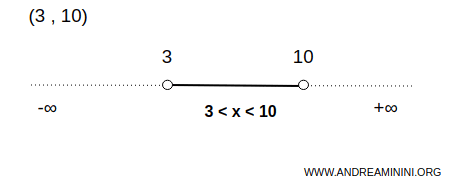
• Mulțime închisă

  O mulțime închisă este o mulțime care conține în întregime punctele sale de frontieră.

  În mod formal, o mulțime \(B\) dintr-un spațiu topologic \(X\) este închisă dacă complementara sa în \(X\) - adică mulțimea punctelor \(u \in X\) care nu aparțin lui \(B\) - este o mulțime deschisă. O altă proprietate fundamentală a mulțimilor închise este aceea că ele conțin toate punctele lor de aderență.
  

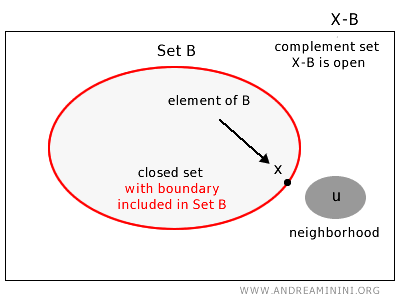
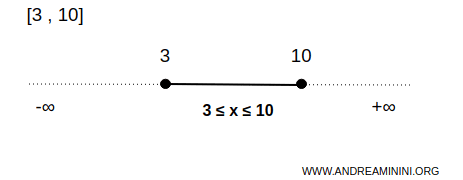
  Exemplu. Considerăm din nou cazul intervalelor reale. Intervalul închis \( [3,10] \) cuprinde toate numerele reale \( x \) pentru care \( 3 \leq x \leq 10 \), inclusiv capetele 3 și 10. Spre deosebire de intervalul deschis, aceste capete fac parte din mulțime. Prin urmare, orice vecinaj al acestor puncte conține elemente din \( B \). De exemplu, intervalul centrat în 3, cu rază \( 0{,}01 \), adică \( [2{,}99, 3{,}01] \), include puncte din afara lui \( B \), ceea ce arată că 3 este un punct de frontieră - însă inclus în mulțime. Acest exemplu este reprezentativ pentru o mulțime închisă într-un spațiu unidimensional.
  

De ce este importantă distincția dintre mulțimile deschise și cele închise ?

Distincția dintre mulțimile deschise și cele închise se află în centrul multor domenii matematice, precum analiza funcțională, geometria diferențială sau teoria grupurilor topologice. Înțelegerea acestor concepte permite descrierea precisă a structurii interne a spațiilor și formularea proprietăților fundamentale precum continuitatea, compactitatea și conexitatea.

Observații

Câteva precizări suplimentare :

• Mulțimi clopen și mulțimi nici deschise, nici închise
  În anumite spații topologice, o mulțime poate fi simultan deschisă și închisă. Astfel de mulțimi se numesc mulțimi clopen. Există, de asemenea, mulțimi care nu sunt nici deschise, nici închise.

  De exemplu, în orice spațiu topologic, mulțimea vidă și întregul spațiu sunt, în mod necesar, atât deschise, cât și închise. Acestea reprezintă cele mai simple și mai fundamentale exemple de mulțimi clopen.

Și așa mai departe.