Submulțimi proprii
Ce este o submulțime proprie?
O mulțime A se numește submulțime proprie a unei mulțimi B dacă:
- toate elementele lui A se regăsesc în B;
- dar B conține cel puțin un element care nu aparține lui A.
Această situație definește o incluziune strictă.
Este un caz particular de incluziune, notat cu simbolul ⊂.
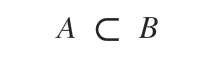
Această notație se citește: „mulțimea A este o parte proprie a mulțimii B” sau „mulțimea A este inclusă strict în mulțimea B”.
Incluziunea strictă presupune ca mulțimile să fie diferite, adică A≠B.
Diferența dintre incluziunea obișnuită și cea strictă: În incluziunea strictă (A⊂B), mulțimile A și B sunt întotdeauna diferite (A≠B), deoarece B are cel puțin un element absent din A. În incluziunea obișnuită (A⊆B), mulțimile pot fi și identice (A=B). Astfel, dacă A este inclusă strict în B (A⊂B), este automat adevărată și incluziunea obișnuită (A⊆B). În schimb, dacă A este inclusă în B în sens obișnuit (A⊆B), nu rezultă neapărat că există o incluziune strictă, deoarece A și B ar putea fi egale.
Exemplu
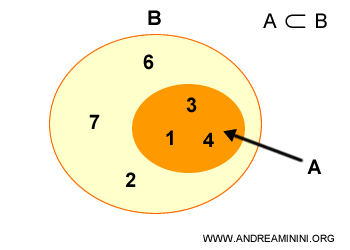
Mulțimea A are trei elemente, iar mulțimea B are șase:
$$ A = \{ 1,3,4 \} $$
$$ B = \{ 1,3,4,2,6,7 \} $$
Prima condiție este îndeplinită: toate elementele lui A se regăsesc în B.
$$ A = \{ 1,3,4 \} ⊂ B $$
A doua condiție este de asemenea îndeplinită: B conține elemente care nu se află în A.
În acest caz, {2,6,7} aparțin lui B, dar nu și lui A:
$$ B = \{ 1,3,4,\color{red}2,\color{red}6,\color{red}7 \} $$
Prin urmare, A este inclusă strict în B, adică A este o submulțime proprie a lui B:
$$ A ⊂ B $$
Și așa mai departe.