Teoria mulțimilor
Teoria mulțimilor își are fundamentul în utilizarea conceptului de mulțime în cadrul limbajului logico-matematic.
Definiția unei mulțimi
O mulțime este o colecție de obiecte, denumite elemente sau membri, care au în comun o anumită proprietate. Poate fi numită, de asemenea, clasă, ansamblu sau familie.
Acest concept este considerat primitiv, deoarece nu poate fi definit prin intermediul altor concepte.
În cadrul unei mulțimi, ordinea elementelor nu are relevanță.
Definiția unei mulțimi în matematică
În matematică, o mulțime reprezintă un grup de obiecte pentru care există un criteriu obiectiv ce permite stabilirea apartenenței sau neapartenenței fiecărui obiect la grupul respectiv.
Atunci când vorbim despre o mulțime matematică, ne referim la un ansamblu bine determinat, ale cărui elemente respectă toate același criteriu obiectiv de apartenență.
Mulțimile definite pe baza unor criterii subiective nu sunt considerate mulțimi matematice.
În continuare, prin termenul „mulțime” voi desemna exclusiv mulțimile matematice.
Exemplu. Mulțimea numerelor prime este o mulțime matematică, deoarece criteriul de apartenență este obiectiv: include toate numerele naturale divizibile doar cu 1 și cu ele însele. $$ I = \{ 2 , 3, 5, 7, 11, ... \} $$ În schimb, mulțimea „celor mai frumoase melodii” nu este o mulțime matematică, întrucât criteriul este subiectiv și diferă de la o persoană la alta.
Reprezentarea mulțimilor
În limbajul logico-matematic, mulțimile se notează cu litere majuscule (A, B, C, D, ...).
Elementele unei mulțimi se notează, în schimb, cu litere minuscule (a, b, c, d, ...).
Simbolurile apartenenței și neapartenenței
Simbolul pentru apartenență la o mulțime este ∈.
Se citește „elementul x aparține mulțimii A”.
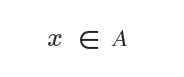
Simbolul pentru neapartenență este ∉.
Se citește „elementul x nu aparține mulțimii A”.
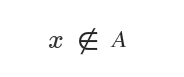
Exemplu. Considerăm mulțimea B a numerelor pare de la 1 la 9. $$ B = \{ \ 2 \ , \ 4 \ , \ 6 \ , \ 8 \ \} $$ Pentru a arăta că numărul 2 aparține lui B, scriem $$ 2 \in B $$ Pentru a arăta că numărul 3 nu aparține lui B, scriem $$ 3 \notin B $$
Reprezentarea grafică
O mulțime poate fi reprezentată grafic prin intermediul diagramelor Euler-Venn, numite și cercuri Euler.
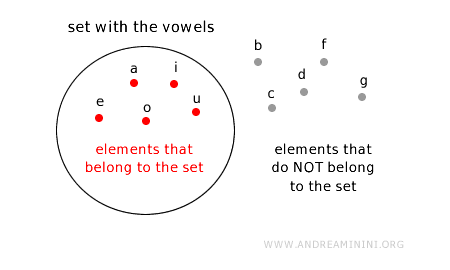
Fiecare mulțime este reprezentată printr-un cerc, o elipsă sau o figură geometrică închisă.
Elementele mulțimii se plasează în interiorul cercului.
Cele care nu aparțin mulțimii se plasează în exterior.
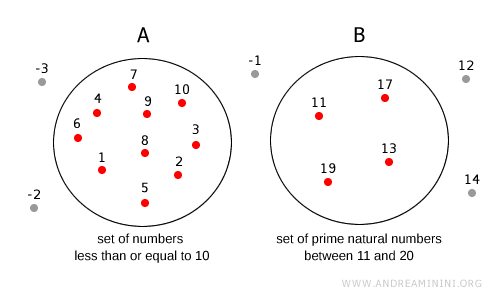
Notă. În mulțimea A se află numerele naturale până la 10. Toate numerele din afara cercului A nu aparțin acesteia. Mulțimea B conține numerele prime cuprinse între 11 și 20. În mod similar, numerele din afara cercului B nu aparțin lui B. Numerele aflate în afara ambelor cercuri (-1, -2, -3, 12, 14, ...) nu aparțin nici mulțimii A, nici mulțimii B.
Dacă un element aparține ambelor mulțimi, acesta trebuie reprezentat în ambele cercuri.
De exemplu, dacă mulțimea B ar fi mulțimea numerelor prime între 1 și 20, mulțimile A și B ar trebui reprezentate intersectându-se.

În acest caz, elementele comune ambelor mulțimi, A⋂B={1, 2, 3, 5, 7}, se află în interiorul ambelor cercuri.
Notă. Diagramele Euler-Venn poartă numele matematicienilor Leonhard Euler (Elveția) și John Venn (Anglia), care le-au folosit pentru prima dată pentru a reprezenta mulțimi.
Reprezentarea tabelară (enumerativă)
O mulțime simplă poate fi prezentată și sub formă tabelară.
În această reprezentare, elementele se scriu între acolade, separate prin virgule.
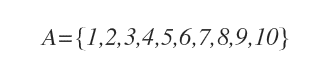
Această metodă se numește și notație enumerativă.
Nu este necesară respectarea unei ordini anume; ordinea elementelor este irelevantă.
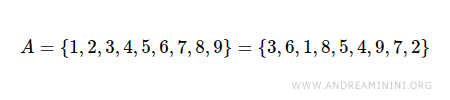
Orice element repetat apare o singură dată în notația enumerativă.
Prin urmare, nu se repetă elementele între acolade.
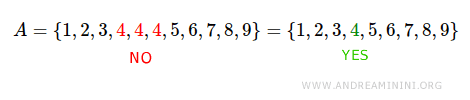
Reprezentarea tabelară este utilă când mulțimea este finită și are puține elemente.
Devine însă dificil de folosit când mulțimea conține un număr mare de elemente.
Notă. Punctele de suspensie ... se folosesc atunci când regula de apartenență este clară, iar elementele omise sunt subînțelese. De exemplu, A={1,2,...,10} reprezintă numerele naturale de la 1 la 10. $$ A = \{ \ 1,2, \ ... \ ,10 \ \} $$ În notația tabelară, ... se folosesc și pentru mulțimi infinite. De exemplu, A={1,2,3,...} desemnează toate numerele naturale de la 1 în sus. $$ A=\{ \ 1,2,3 \ ... \ \} $$
Reprezentarea prin regulă de formare
O mulțime poate fi descrisă și prin notația cu regulă de formare, care se bazează pe proprietatea caracteristică a elementelor sale.
Această metodă este utilă în special când mulțimea are multe elemente sau este infinită.
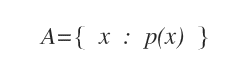
Între acolade se notează regula de apartenență, cunoscută și ca proprietate caracteristică, utilizând limbajul formal al logicii matematice.
Exemplu. În notația prin comprehensiune, numerele naturale de la 1 la 10 se reprezintă astfel: $ A= \{x \in N:0 \lt x \le 10 \} $.
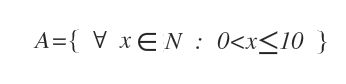
Unde x este o variabilă ce indică orice număr natural x∈N. Simbolul ∀ se citește „pentru orice”. Cele două puncte : se citesc „astfel încât”. Uneori, se folosește și simbolul | cu același sens: „astfel încât”. $$ A = \{ \ \forall \ x \in N \ | \ 0 \lt x \le 10 \} $$ Prin urmare, notația de mai sus se citește astfel: „A este mulțimea numerelor naturale x, astfel încât x este un număr între 0 și 10”.
Avantajele și limitele notațiilor
Notația prin regulă de formare poate fi utilizată pentru a descrie orice tip de mulțime, fie ea finită sau infinită, atâta timp cât elementele pot fi identificate pe baza unuia sau mai multor criterii bine definite.
Notația enumerativă, în schimb, este adecvată doar în următoarele situații:
- când mulțimea este finită și conține un număr redus de elemente
- când mulțimea este finită sau infinită, dar poate fi reprezentată prin indicarea explicită a câtorva elemente, restul fiind deduse implicit.
În sfârșit, notația grafică este deosebit de utilă pentru a ilustra sau a transmite vizual concepte care ar putea fi greu de înțeles exclusiv prin notația logico-matematică.
Mulțimi finite și infinite
O mulțime poate fi finită sau infinită.
- Mulțimea finită conține un număr determinat n de elemente.
Exemplu. Mulțimea cărților dintr-un rucsac este o mulțime finită. Un alt exemplu este mulțimea boabelor de nisip dintr-un recipient.
- Mulțimea infinită cuprinde un număr nelimitat de elemente.
Exemplu. Mulțimea numerelor naturale este infinită, deoarece fiecărui număr natural n îi urmează un succesor n+1. Nu există un număr natural care să fie mai mare decât toate celelalte.
Mulțimile numerice
Mulțimile numerice sunt acele mulțimi alcătuite exclusiv din numere.
Prin convenție, în matematică, aceste mulțimi se notează cu litere mari specifice:
- N - mulțimea numerelor naturale
- Z - mulțimea numerelor întregi
- Q - mulțimea numerelor raționale
- I - mulțimea numerelor iraționale
- R - mulțimea numerelor reale
- C - mulțimea numerelor complexe
Mulțimea vidă
Mulțimea vidă este mulțimea care nu conține niciun element. Se notează cu simbolul Ø. $$ Ø = \{ \ \ \} $$
Uneori, mulțimea vidă este reprezentată prin două acolade goale.
Este o mulțime specială, deoarece este submulțime a oricărei alte mulțimi.
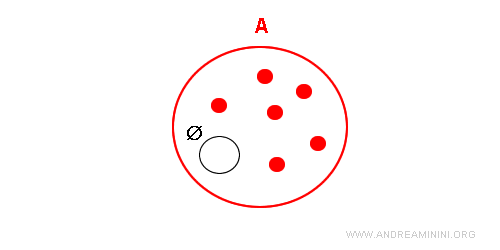
Există o singură mulțime vidă. De exemplu, mulțimea numerelor naturale impare divizibile cu doi este vidă, întrucât niciun număr natural impar nu este divizibil cu doi. În mod similar, mulțimea pătratelor cu trei laturi este vidă, deoarece orice pătrat are patru laturi. În ambele cazuri, vorbim despre aceeași mulțime vidă, chiar dacă regulile de apartenență diferă.
Și așa mai departe.