Cote superioare și inferioare

Analiza conceptului de cote superioare și inferioare

Fie o mulțime A și un subansamblu B ⊆ A.

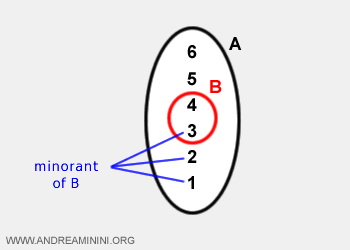
• Un element \( k \in A \) se numește cotă inferioară (sau minorant) al subansamblului B dacă îndeplinește condiția \( k \le b \) pentru orice \( b \in B \).

  Exemplu. Considerăm mulțimea A = {1, 2, 3, 4, 5, 6} și subansamblul B = {3, 4}. Mulțimea cotelor inferioare ale lui B este {1, 2, 3}.
  

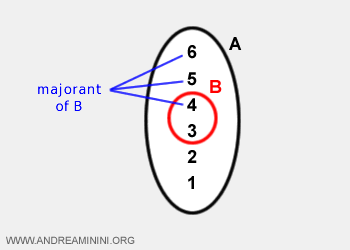
• Un element \( k \in A \) se numește cotă superioară (sau majorant) al subansamblului B dacă îndeplinește condiția \( k \ge b \) pentru orice \( b \in B \).

  Exemplu. Pentru mulțimea A = {1, 2, 3, 4, 5, 6} și subansamblul B = {3, 4}, mulțimea cotelor superioare ale lui B este {4, 5, 6}.
  

Domeniul cotelor superioare și inferioare într-o mulțime

O mulțime poate admite mai multe cote superioare și inferioare sau, în anumite situații, să nu posede niciuna.

Exemple ilustrative

Există mulțimi care admit cote inferioare, dar nu și cote superioare.

Acestea se numesc mulțimi mărginit inferior.

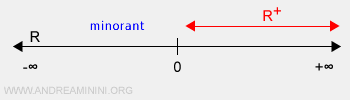
Exemplu de mulțime fără cote superioare. Mulțimea numerelor reale pozitive R⁺, adică intervalul (0,+∞), este un subansamblu al lui R. Ea posedă cote inferioare, precum zero și toate numerele reale negative, deși acestea nu aparțin propriu-zis lui R⁺. De pildă, zero nu face parte din R⁺, iar între zero și orice număr pozitiv se află o infinitate de numere reale. În schimb, R⁺ nu are cote superioare, întrucât se prelungește indefinit către +∞.

Analog, există mulțimi care admit cote superioare, dar nu și cote inferioare.

Acestea se numesc mulțimi mărginit superior.

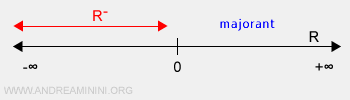
Exemplu de mulțime fără cote inferioare. Mulțimea numerelor reale negative R^-, adică intervalul (-∞,0), este un subansamblu infinit al lui R. Ea are cote superioare, precum zero și toate numerele reale pozitive, însă niciuna dintre acestea nu aparține lui R^-. De exemplu, zero nu se găsește în R^-, iar între zero și orice număr negativ se află infinit de multe numere reale. În schimb, R^- nu posedă cote inferioare, întrucât se extinde nelimitat spre -∞.

Există și mulțimi care sunt mărginit atât superior, cât și inferior.

Acestea se numesc simplu mulțimi mărginit.

Exemplu de mulțime cu cote atât superioare, cât și inferioare. Mulțimea numerelor reale cuprinse între -1 și +1 este un subansamblu al lui R. Ea are o infinitate de cote inferioare situate în intervalul (-∞, -1) și, simetric, o infinitate de cote superioare în intervalul (1,+∞).

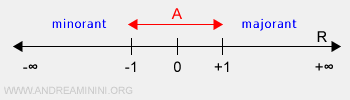
În fine, există mulțimi care nu admit nici cote superioare, nici cote inferioare.

Exemplu de mulțime fără cote. Mulțimea vidă este un subansamblu impropriu al oricărei mulțimi universale și nu posedă nici cote superioare, nici cote inferioare. În mod similar, orice mulțime nemărginită atât superior, cât și inferior - de pildă mulțimea numerelor reale R - este un subansamblu impropriu al ei însăși și, prin urmare, nu are cote.

Și așa mai departe.