Intersecția Mulțimilor

Intersecția a două mulțimi A și B este mulțimea formată din toate elementele care aparțin simultan atât lui A, cât și lui B.

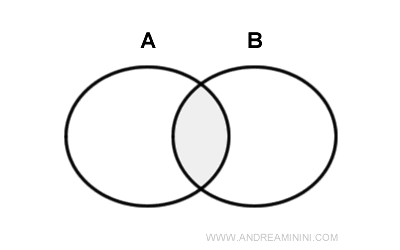
Simbolul folosit pentru intersecție este ⋂.

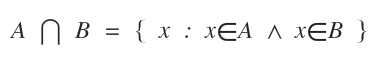
Această notație se citește „intersecția lui A și B” sau „A intersectat cu B”.

Intersecția mai multor mulțimi. Atunci când se intersectează mai mult de două mulțimi, se poate utiliza o notație mai compactă pentru a reprezenta intersecția: $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

Dacă două mulțimi nu au elemente comune, intersecția A⋂B este mulțimea vidă.

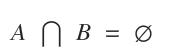
În acest caz, mulțimile se numesc disjuncte.

Exemplu practic

Să presupunem că avem două mulțimi finite A și B:

$$ A = \{ 2,5,6,7,8 \} $$

$$ B = \{ 1,3,4,6,7,9 \} $$

Observăm că cele două mulțimi au în comun două elemente.

$$ A = \{ 2,5,\color{red}6,\color{red}7,8 \} $$

$$ B = \{ 1,3,4,\color{red}6,\color{red}7,9 \} $$

Prin urmare, intersecția lui A și B este formată din elementele 6 și 7:

$$ A \cap B = \{ 6,7 \} $$

Mai jos este prezentată intersecția reprezentată grafic printr-o diagramă Euler - Venn.

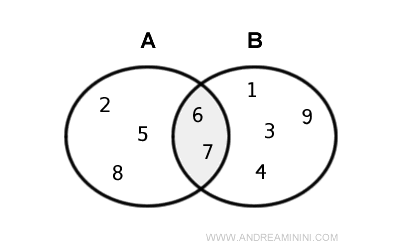
Tipuri de intersecție

În funcție de relația dintre mulțimi, intersecția poate avea forme diferite:

• Intersecția A⋂B este un subansamblu propriu al ambelor mulțimi.

  Exemplu. Pentru $$ A = \{ 2,5,6,7,8 \} $$ și $$ B = \{ 1,3,4,6,7,9 \} $$ avem $$ A \cap B = \{ 6,7 \} $$. În acest caz, intersecția este un subansamblu propriu al lui A și al lui B: $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$. Este același exemplu prezentat mai devreme.
  

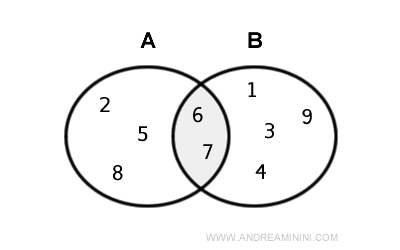
• Intersecția A⋂B este un subansamblu propriu al uneia dintre mulțimi și un subansamblu impropriu al celeilalte. Acest lucru se întâmplă atunci când una dintre mulțimi este inclusă complet în cealaltă, adică atunci când A ⊆ B.

  Exemplu. Pentru $$ A = \{ 3,6,7 \} $$ și $$ B = \{ 1,3,4,6,7,9 \} $$ intersecția este $$ A \cap B = \{ 3,6,7 \} $$. Grafic:
  
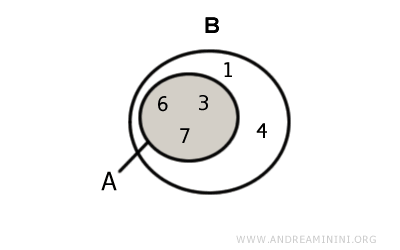
  În acest caz, intersecția este un subansamblu impropriu al lui A, deoarece coincide complet cu acesta: $$ A \cap B = A $$. În schimb, este un subansamblu propriu al lui B, întrucât B conține și alte elemente care nu se află în A: $$ A \cap B ⊂ B $$

• Intersecția A⋂B este un subansamblu impropriu al ambelor mulțimi. Acest lucru se poate întâmpla în două situații:
  
  A] Când mulțimile sunt disjuncte, intersecția este mulțimea vidă, care este un subansamblu impropriu al oricărei mulțimi.

  Exemplu. Pentru $$ A = \{ 2,5,8 \} $$ și $$ B = \{ 1,3,4,6,7,9 \} $$ intersecția este $$ A \cap B = \{ \ \ \} = Ø $$. Așadar, A și B nu au elemente comune.
  
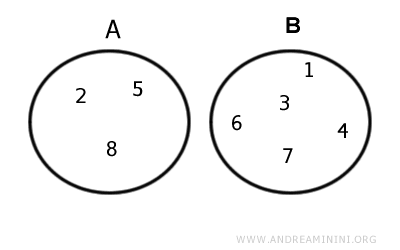
  Deoarece mulțimea vidă este un subansamblu impropriu al oricărei mulțimi, ea este improprie și pentru A, și pentru B: $$ A \cap B ⊂ A $$ $$ A \cap B ⊂ B $$

  B] Când mulțimile sunt identice. În acest caz, intersecția lor este egală cu ambele mulțimi.

  Exemplu. Pentru $$ A = \{ 1,2,3,4 \} $$ și $$ B = \{ 1,2,3,4 \} $$ intersecția este egală cu A și B: $$ A \cap B = A = B $$. A și B conțin exact aceleași elemente, deci sunt mulțimi identice.
  
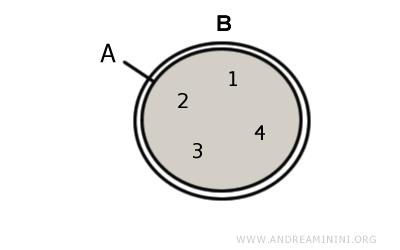
  Când două mulțimi sunt identice, ele sunt subansambluri improprii una ale celeilalte.

Proprietăți ale intersecției

Intersecția mulțimilor respectă proprietăți similare cu cele ale adunării și înmulțirii numerelor:

• Proprietatea comutativă
  Ordinea mulțimilor nu influențează rezultatul: $$ A \cap B = B \cap A $$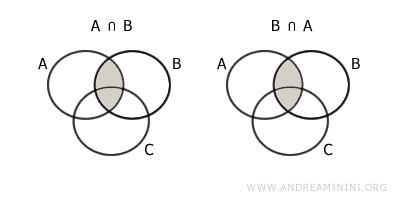

  

• Proprietatea asociativă
  $$ (A \cap B) \cap C = A \cap (B \cap C) $$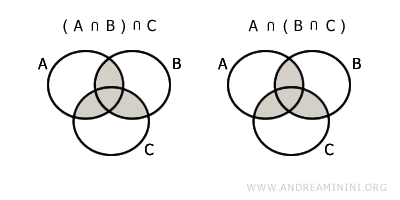

  

• Proprietatea distributivă față de reuniune
  $$ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) $$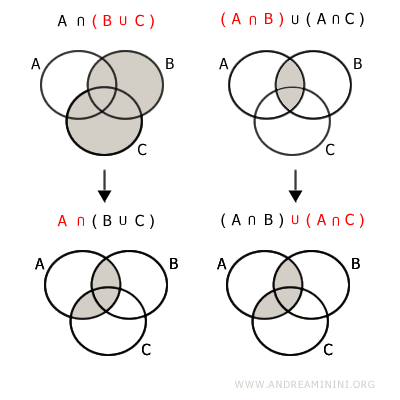

  

Și așa mai departe.