Mulțimea Vidă

Mulțimea vidă este acea mulțime care nu conține niciun element. Ea se notează prin simbolul Ø sau printr-o pereche de acolade goale { }.

Simbolul mulțimii vide, ∅, se citește „mulțimea vidă” sau, mai simplu, „vidă”.

Un exemplu practic

Mulțimea numerelor naturale impare divizibile cu doi este vidă, deoarece niciun număr impar nu poate fi divizibil cu doi.

Există o singură mulțime vidă. Mulțimea numerelor naturale impare divizibile cu doi este o mulțime vidă. În mod similar, mulțimea „triunghiurilor” cu patru laturi este, de asemenea, o mulțime vidă. În ambele situații, deși criteriile de apartenență diferă, ne referim la aceeași mulțime vidă. $$ Ø = \{ \ \ \} $$

Noțiunea de mulțime vidă ridică întrebări interesante despre ideea de existență în matematică, fiind un obiect care, deși nu conține nimic, există totuși.

Am putea-o descrie drept „nimicul” care, paradoxal, reprezintă „ceva” în cadrul universului matematic.

Mulțimea vidă ca submulțime improprie

Mulțimea vidă este o submulțime improprie a oricărei mulțimi.

Demonstrație

Pentru a demonstra acest fapt, folosim metoda reducerii la absurd.

Fie A o mulțime oarecare. Să presupunem, contrar celor de mai sus, că mulțimea vidă nu este o submulțime a lui A.

Această presupunere ar implica existența cel puțin a unui element în mulțimea vidă care să nu aparțină lui A.

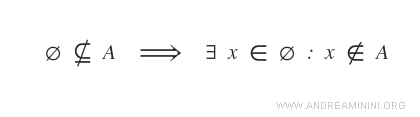
Însă acest lucru este imposibil, deoarece mulțimea vidă nu conține niciun element.

Rezultă, prin urmare, că ipoteza inițială este falsă, iar concluzia corectă este că mulțimea vidă este, într-adevăr, o submulțime a lui A.

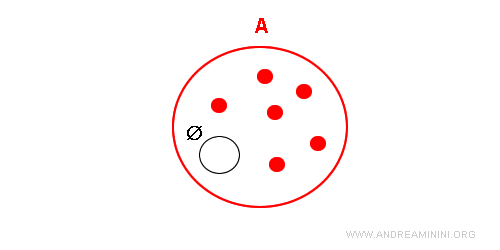
Astfel, mulțimea vidă este considerată o submulțime improprie a oricărei mulțimi.

O altă demonstrație. Reuniunea oricărei mulțimi A cu una dintre submulțimile sale B⊆A este întotdeauna egală cu mulțimea A. $$ A \cup B = A $$ În particular, dacă B este mulțimea vidă, atunci: $$ A \cup Ø = A $$ Rezultă că mulțimea vidă este submulțime a lui A.

Proprietăți esențiale ale mulțimii vide

• Unicitatea
  În matematică, există o singură mulțime vidă. Indiferent de contextul în care este menționată, ea reprezintă același obiect matematic.

  Această unicitate este importantă deoarece asigură că toate proprietățile asociate mulțimii vide sunt universale și independente de context sau notație. Din acest motiv, ne referim mereu la ea la singular: „mulțimea vidă” și nu „mulțimile vide”.

• Submulțime a oricărei mulțimi
  Este considerată o submulțime improprie a oricărei alte mulțimi.

  Conform definiției, o mulțime \(A\) este submulțime a unei mulțimi \(B\) dacă fiecare element al lui \(A\) aparține și lui \(B\). Cum mulțimea vidă, \(\emptyset\), nu are elemente, această condiție este îndeplinită automat pentru orice \(B\).

• Element neutru la reuniune
  Reuniunea unei mulțimi A cu mulțimea vidă Ø este chiar A, deoarece mulțimea vidă nu adaugă elemente. $$ A \cup \emptyset = A $$

  Exemplu. Dacă A = {a, b, c} și B = { } (mulțimea vidă), atunci reuniunea lor este A: $$ A \cup B = \{ a,b,c \} \cup \{ \ \} = \{a,b,c \} = A $$ $$ B \cup A = \{ \ \} \cup \{ a,b,c \} = \{a,b,c \} = A $$

• Element absorbant la intersecție
  Intersecția oricărei mulțimi A cu mulțimea vidă Ø este întotdeauna mulțimea vidă. $$ A \cap \emptyset = \emptyset $$

  Exemplu. Dacă A = {a, b, c} și B = { }, atunci: $$ A \cap B = \{ a,b,c \} \cap \{ \ \} = \emptyset $$ $$ B \cap A = \{ \ \} \cap \{ a,b,c \} = \emptyset $$

• Complement
  Complementul mulțimii vide într-o mulțime universală \( U \) este chiar mulțimea \( U \).

  $$ U \setminus ∅ = U $$

• Produs cartezian
  Produsul cartezian al oricărei mulțimi A cu mulțimea vidă ∅ este întotdeauna mulțimea vidă. $$ A \times ∅ = ∅ $$ $$ ∅ \times A = ∅ $$
• Mulțimea putere
  Mulțimea putere a mulțimii vide conține un singur element: chiar mulțimea vidă. $$ P(∅) = \{\emptyset \} $$
• Deschisă și închisă în topologie
  În orice spațiu topologic, mulțimea vidă este simultan deschisă și închisă.
• Este mulțimea vidă o submulțime proprie sau improprie?
  În unele texte, mulțimea vidă (∅) este clasificată ca submulțime improprie, iar în altele ca submulțime proprie. Această diferență se datorează definiției particulare adoptate pentru termenul „submulțime proprie”.

Și lista poate continua.