Partiția unei Mulțimi

• O partiție P(A) a unei mulțimi A este o colecție de submulțimi ale lui A care îndeplinește următoarele condiții:


• niciuna dintre submulțimi nu este mulțimea vidă
• reuniunea tuturor submulțimilor este întreaga mulțime A
• submulțimile sunt disjuncte două câte două, adică nu au elemente comune

Împărțirea unei mulțimi în două submulțimi se numește bipartiție.

Împărțirea într-o colecție de trei submulțimi se numește tripartiție.

În general, o împărțire în k submulțimi se numește k-partiție.

Notă: O mulțime poate fi particionată în mai multe moduri. O mulțime cu k elemente admite k! partiții distincte.

Un Exemplu

Să considerăm mulțimea finită A cu 5 elemente:

$$ A = \{ 1,2,3,4,5 \} $$

O posibilă partiție este următoarea bipartiție:

$$ P(A) = \{ \ \{ 1,2,3 \} \ , \ \{ 4,5 \} \ \} $$

Reprezentată printr-o diagramă Euler - Venn, această bipartiție arată astfel:

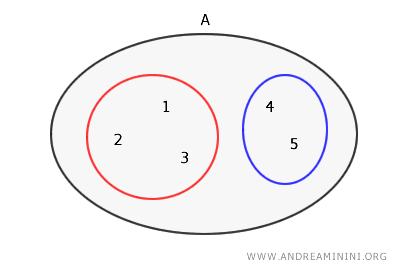
Verificare: Partiția conține două submulțimi nevide, {1,2,3} și {4,5}, care sunt disjuncte: $$ \{ 1,2,3 \} \cap \{4,5 \} = Ø $$ Reuniunea lor este întreaga mulțime A: $$ \{ 1,2,3 \} \cup \{4,5 \} = \{ 1,2,3,4,5 \} = A $$

Deoarece mulțimea A are 5 elemente, ea admite 52 de partiții posibile.

De exemplu, o altă bipartiție este:

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4,5 \} \ \} $$

O altă posibilitate este următoarea tripartiție:

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3,4 \} \ , \ \{ 5 \} \ \} $$

De asemenea, putem împărți A în 4 submulțimi:

$$ P(A) = \{ \ \{ 1,2 \} \ , \ \{ 3 \} \ , \ \{ 4 \} \ , \{ 5 \} \ \} $$

În total, există 52 de moduri diferite de a particiona elementele lui A.

Calculul Numărului de Partiții

Numărul de partiții ale unei mulțimi finite \( A \) cu \( n \) elemente este dat de numerele lui Bell, notate \( B_n \). Acestea se pot determina prin formula recursivă, având condiția inițială \( B_0 = 1 \):

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

În această formulă:

• \( \binom{n-1}{k} \) este coeficientul binomial care indică numărul de moduri în care pot fi alese \( k \) elemente dintr-o mulțime de \( n-1 \) elemente;
• \( B_k \) este numărul lui Bell deja calculat pentru mulțimi cu \( k \) elemente.

Așadar, \( B_n \) exprimă numărul de moduri posibile de a împărți o mulțime cu \( n \) elemente în submulțimi disjuncte.

Numerele lui Bell pot fi calculate și cu ajutorul formulei exponențiale a lui Dobinski:

$$ B_n = \frac{1}{e} \sum_{k=0}^{\infty} \frac{k^n}{k!} $$

În practică însă, se folosește mai des formula recursivă, prin care obținem, de exemplu, \( B_5 = 52 \) pentru mulțimea \( A = \{1,2,3,4,5\} \).

Exemplu

Să determinăm numărul de partiții ale mulțimii \( A \), care conține \( n = 5 \) elemente:

$$ A = \{ 1,2,3,4,5 \} $$

Pentru aceasta folosim formula recursivă:

$$ B_n = \sum_{k=0}^{n-1} \binom{n-1}{k} B_k $$

În cazul nostru, pentru \( n=5 \):

$$ B_5 = \sum_{k=0}^{4} \binom{4}{k} B_k $$

Șirul numerelor lui Bell începe cu valoarea inițială:

$$ B_0 = 1 $$

Calculăm succesiv valorile intermediare.

1. Pentru \( B_1 \):

$$ B_1 = \binom{0}{0} B_0 = 1 \times 1 = 1 $$

2. Pentru \( B_2 \):

$$ B_2 = \binom{1}{0} B_0 + \binom{1}{1} B_1 = 1 \times 1 + 1 \times 1 = 2 $$

3. Pentru \( B_3 \):

$$ B_3 = \binom{2}{0} B_0 + \binom{2}{1} B_1 + \binom{2}{2} B_2 $$

$$ B_3 = 1 \times 1 + 2 \times 1 + 1 \times 2 = 5 $$

4. Pentru \( B_4 \):

$$ B_4 = \binom{3}{0} B_0 + \binom{3}{1} B_1 + \binom{3}{2} B_2 + \binom{3}{3} B_3 $$

$$ B_4 = 1 \times 1 + 3 \times 1 + 3 \times 2 + 1 \times 5 = 15 $$

5. Pentru \( B_5 \):

$$ B_5 = \binom{4}{0} B_0 + \binom{4}{1} B_1 + \binom{4}{2} B_2 + \binom{4}{3} B_3 + \binom{4}{4} B_4 $$

$$ B_5 = 1 \times 1 + 4 \times 1 + 6 \times 2 + 4 \times 5 + 1 \times 15 = 52 $$

Rezultatul este:

$$ B_5 = 52 $$

Așadar, pentru \( n=5 \), numărul lui Bell este 52, ceea ce înseamnă că există 52 de moduri distincte de a particiona mulțimea \( A = \{ 1,2,3,4,5 \} \).

Observații

• Partiția trivială
  Orice mulțime \( X \) are o partiție trivială, formată doar din ea însăși: $$ P(A) = \{ A \} $$

  Exemplu: pentru mulțimea $$ A = \{ 1,2,3,4,5 \} $$ partiția trivială este: $$ P(A) = \{ \ \{ 1,2,3,4,5 \} \ \} $$

• Partiția în singletons
  O altă partiție extremă este împărțirea într-o colecție de submulțimi unitare (singletons): $$ P(A) = \{ \{ a_1 \}, \{ a_2 \}, \dots, \{ a_n \} \} $$

  Exemplu: pentru $$ A = \{ 1,2,3,4,5 \} $$ partiția în singletons este: $$ P(A) = \{ \{1\}, \{2\}, \{3\}, \{4\}, \{5\} \} $$

Între aceste două extreme (partiția trivială și partiția în singletons) se regăsesc toate celelalte posibilități, în număr de 52 pentru cazul analizat.