Mulțimea Putere (Mulțimea tuturor submulțimilor)

Ce reprezintă mulțimea tuturor submulțimilor?

Mulțimea putere, notată \( P(A) \), este mulțimea care reunește toate submulțimile lui \( A \), atât proprii cât și improprii. $$ P(A) = \{ S \mid S \subseteq A \} $$ Ea este cunoscută și sub denumirea de mulțimea putere.

Fiecare submulțime \( S = \{s_1, \dots\} \) constituie o parte a mulțimii \( A \).

$$ S \subseteq A $$

Prin urmare, orice submulțime \( S \) este un element al mulțimii tuturor submulțimilor \( P(A) \).

$$ S \in P(A) $$

Notă. În acest context, submulțimea este considerată un element pentru că aparține lui \( P(A) \). De aceea folosim simbolul apartenenței \( S \in P(A) \). Totuși, \( S \) nu este inclusă în \( P(A) \), ci în \( A \), adică \( S \subseteq A \).

Exemplu practic de mulțime a tuturor submulțimilor

Să luăm o mulțime \( A \) alcătuită din elementele \( a \) și \( b \).

$$ A = \{ a,b \} $$

Elementele \( a \) și \( b \) fac parte din \( A \).

$$ a,b \in A $$

Mai jos este redată diagrama lui Venn pentru această mulțime.

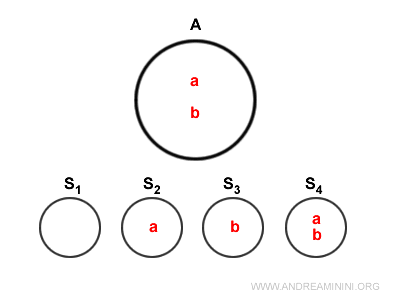
Toate submulțimile lui \( A \) intră în componența mulțimii putere \( P(A) \).

$$ \{ \} \\ \{ a \} \\ \{ b \} \\ \{ a,b \} $$

Prin urmare, mulțimea tuturor submulțimilor este formată din următoarele elemente:

$$ P(A) = \{ \{ \} , \{ a \} , \{ b \} , \{ a,b \} \} $$

sau, echivalent:

$$ P(A) = \{ ∅ , \{ a \} , \{ b \} , A \} $$

Submulțimile \( \{ a \} \) și \( \{ b \} \) sunt submulțimi proprii ale lui \( A \).

În schimb, \( ∅ \) și \( A \) sunt submulțimi improprii ale lui \( A \).

Notă. Deoarece toate aceste elemente aparțin lui \( P(A) \), putem nota: $$ ∅ , \{ a \} , \{ b \} , A \in P(A) $$

Mai jos este ilustrată diagrama lui Venn a mulțimii putere \( P(A) \).

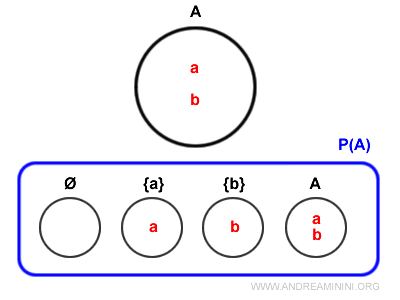
Observăm că și mulțimea \( A \) însăși este un element al lui \( P(A) \), deoarece orice mulțime este o submulțime improprie a ei înseși.

De ce apare și mulțimea vidă?

În teoria mulțimilor, mulțimea vidă \( ∅ \) este submulțime a oricărei mulțimi.

Așadar, mulțimea vidă \( ∅ \) este și ea o submulțime a lui \( A \).

Prin urmare, \( ∅ \) se regăsește în mulțimea tuturor submulțimilor \( P(A) \).

Mulțimea tuturor submulțimilor mulțimii vide

Dacă mulțimea \( A \) este vidă, adică \( A = ∅ \), atunci mulțimea ei putere este:

$$ P(A) = \{ ∅ \} $$

Este esențial de precizat că \( \{∅\} \) nu reprezintă mulțimea vidă, ci o mulțime ce conține mulțimea vidă ca unic element.

De ce se numește mulțimea tuturor submulțimilor „mulțime putere”?

Mulțimea tuturor submulțimilor este denumită mulțime putere datorită unei proprietăți fundamentale.

Dacă o mulțime \( A \) are \( n \) elemente, atunci mulțimea sa putere \( P(A) \) conține exact \( 2^n \) elemente.

Exemplu

Mulțimea \( A = \{a, b\} \) are \( n = 2 \) elemente.

Prin urmare, mulțimea putere \( P(A) \) conține 4 elemente:

$$ 2^n = 2^2 = 4 $$

Iar această regulă se verifică pentru orice mulțime.