Extremele unei mulțimi

Definiția extremelor

Orice mulțime nevidă are întotdeauna un suprem (cea mai mică limită superioară) și un infim (cea mai mare limită inferioară).

• În mulțimile mărginite, extremele sunt numere finite.
• În mulțimile nemărginite, extremele sunt redate prin simbolurile infinitului pozitiv sau negativ (±∞).

O mulțime poate fi mărginită superior (are un suprem finit) și nemărginită inferior (infimul este -∞), sau invers.

Notă: Suprema și infimul unei mulțimi pot să aparțină sau nu mulțimii respective.

Cea mai bună cale de a înțelege noțiunile de infim și suprem este prin exemple concrete.

Infimul

Fie o mulțime A și un submulțime B $$ B ⊆ A $$, infimul lui B este un element a∈A care este mai mic sau egal decât orice element b∈B. $$ inf(B) = a \le b \:\:\: a \in A, b \in B $$

• În cazul mulțimilor mărginitE, infimul este cel mai mare dintre limitările inferioare (minorante).

  De exemplu, infimul lui B este numărul 3.
  

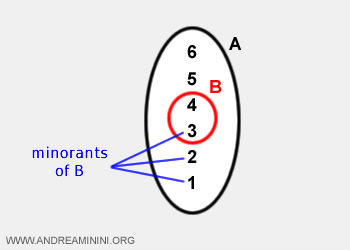
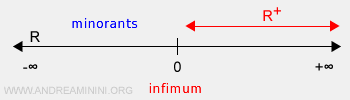
• În cazul mulțimilor nemărginite, infimul este minus infinit (-∞).

Exemplul 1

Mulțimea A este mulțimea tuturor numerelor reale R pe intervalul (-∞,+∞).

Mulțimea B este alcătuită din 7 numere reale și reprezintă un submulțime al lui A.

$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$

Infimul lui B este numărul 3.

$$ inf(B) = 3 \le b \:\:\: \forall \: b \in B $$

deoarece 3 este cel mai mic element al lui B.

Notă: În acest caz, infimul inf(B)=3 aparține mulțimii B, dar nu este obligatoriu să fie așa.

Exemplul 2

Mulțimea A este mulțimea tuturor numerelor reale R pe intervalul (-∞,+∞).

Mulțimea B este mulțimea numerelor reale pozitive R⁺, un submulțime al lui A.

Infimul lui B este zero.

$$ inf(B) \le b \:\:\: \forall \: b \in B $$

El reprezintă cea mai mare limită inferioară a mulțimii R⁺.

Notă: În acest caz, infimul inf(B)=0 nu aparține mulțimii B (R⁺), întrucât există o infinitate de numere pozitive arbitrar de apropiate de zero.

Supremul

Fie o mulțime A și un submulțime B $$ B ⊆ A $$, supremul lui B este un element a∈A care este mai mare sau egal decât orice element b∈B. $$ sup(B) = a \ge b \:\:\: a \in A, b \in B $$

• În cazul mulțimilor mărginitE, supremul este cel mai mic dintre limitările superioare (majorante).

  De exemplu, supremul lui B este 9.
  

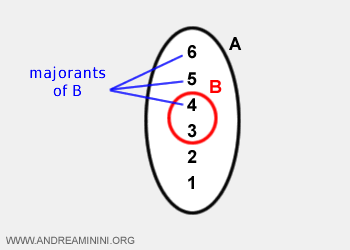
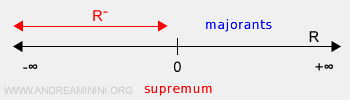
• În cazul mulțimilor nemărginite, supremul este plus infinit (+∞).

Exemplul 1

Mulțimea A este mulțimea tuturor numerelor reale R pe intervalul (-∞,+∞).

Mulțimea B este alcătuită din 7 numere reale și reprezintă un submulțime al lui A.

$$ B = \{ 3, 4, 7, 5, 8, 9, 6 \} $$

Supremul lui B este numărul 9.

$$ sup(B) = 9 \ge b \:\:\: \forall \: b \in B $$

deoarece 9 este cel mai mare element al lui B.

Notă: În acest caz, supremul sup(B)=9 aparține mulțimii B, dar nu este obligatoriu să fie așa.

Exemplul 2

Mulțimea A este mulțimea tuturor numerelor reale R pe intervalul (-∞,+∞).

Mulțimea B este mulțimea numerelor reale negative R^-, un submulțime al lui A.

Limita inferioară a lui B este minus infinit.

$$ inf(B) = - \infty \le b \:\:\: \forall \: b \in B $$

Notă: În acest caz, limita inferioară inf(B)=-∞ „aparține” lui B (R^-) în sensul că mulțimea numerelor reale negative nu are o limită inferioară efectivă. Totuși, limita superioară sup(B)=0 nu aparține lui B (R^-), deoarece 0 nu este un număr real negativ.

Și așa mai departe.