Mulțime compactă

Într-un spațiu precum \(\mathbb{R}^n\), o mulțime compactă este o mulțime care este simultan închisă și mărginită.

Închisă: o mulțime este închisă dacă include toate punctele sale de acumulare, adică dacă conține întreaga sa frontieră.
Mărginită: o mulțime este mărginită dacă se află în întregime în interiorul unei bile cu rază finită.

Într-un cadru mai general, adică în topologie, o mulțime \(K\) se numește compactă dacă orice acoperire deschisă a lui \(K\) conține o subacoperire finită care îl acoperă complet.

În spațiul \(\mathbb{R}^n\), cele două definiții sunt echivalente, însă în spații topologice mai abstracte pot conduce la rezultate diferite.

Observație: Compacitatea oferă mulțimilor proprietăți fundamentale. De exemplu, orice funcție continuă definită pe o mulțime compactă atinge întotdeauna o valoare maximă și una minimă (teorema lui Weierstrass), iar orice șir de puncte dintr-o astfel de mulțime are o subsecvență convergentă (teorema lui Bolzano-Weierstrass). În consecință, o funcție continuă pe o mulțime compactă are întotdeauna extreme, fără excepție.

Exemple

Exemplul 1

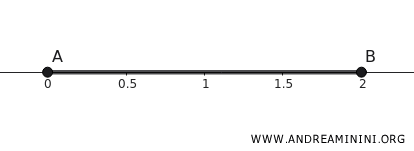
Să considerăm intervalul \([0,2]\) din axa reală \(\mathbb{R}\).

Definim mulțimea:

\[ K = \{ x \in \mathbb{R} \mid 0 \leq x \leq 2 \} \]

Această mulțime este compactă din următoarele motive:

Este închisă, deoarece include capetele intervalului \(0\) și \(2\).
Este mărginită, întrucât toate valorile lui \(x\) sunt cuprinse între \(0\) și \(2\), iar mulțimea nu se extinde la infinit.

exemplu de mulțime compactă

Exemplul 2

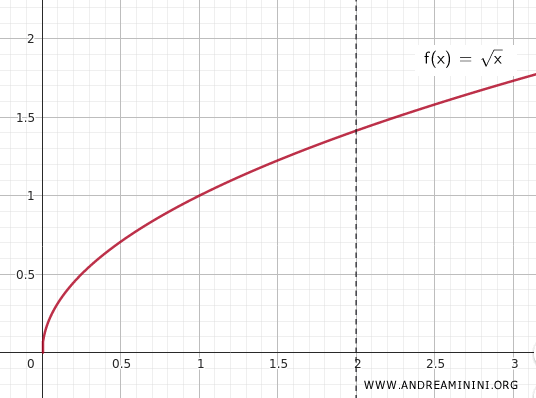
Considerăm acum funcția continuă \(f(x) = \sqrt{x}\), definită pe mulțimea \(K\).

Deoarece \(f(x)\) este continuă pe o mulțime compactă, teorema lui Weierstrass garantează că funcția atinge atât un minim, cât și un maxim pe \(K\).

Într-adevăr, pe intervalul \([0,2]\), funcția are valoarea minimă în \(x = 0\) (adică \(0\)) și valoarea maximă în \(x = 2\) (adică \(\sqrt{2}\)).

graficul unei funcții continue definite pe o mulțime compactă

Exemplul 3

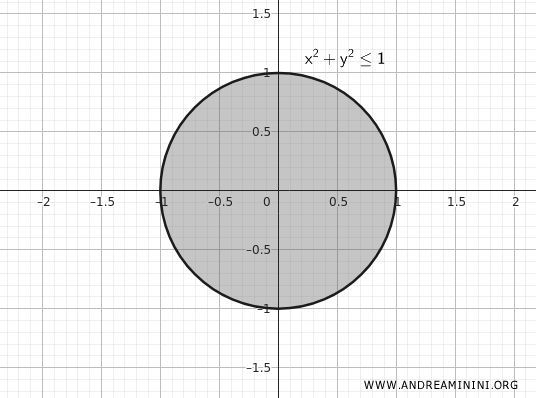
Să analizăm acum discul închis de rază \(1\), centrat în origine, din planul \(\mathbb{R}^2\).

Definim mulțimea:

\[ K = \{ (x,y) \in \mathbb{R}^2 \mid x^2 + y^2 \leq 1 \} \]

Această mulțime este de asemenea compactă, pentru că:

Este închisă, întrucât conține toate punctele de pe frontieră, definite prin ecuația \(x^2 + y^2 = 1\).
Este mărginită, deoarece niciun punct nu se află la o distanță mai mare de \(1\) față de origine \((0,0)\).

disc închis care ilustrează o mulțime compactă

Și așa mai departe.