Operații cu Mulțimi

Operațiile fundamentale cu mulțimi sunt reuniunea, intersecția și diferența.

Pentru a ilustra cât mai clar aceste operații, recurgem în principal la diagramele lui Venn, deoarece ele oferă o reprezentare vizuală intuitivă. În general, reprezentarea grafică este mai sugestivă și mai ușor de înțeles decât simpla notație matematică.

Reuniunea

Fie două mulțimi A și B. Reuniunea lor este mulțimea tuturor elementelor care se află în A, în B sau în ambele simultan.

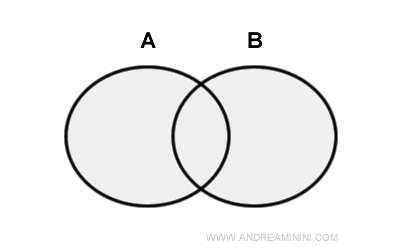
Simbolul utilizat pentru reuniune este ∪.

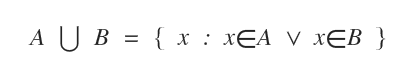
În reuniune, elementele comune celor două mulțimi sunt luate o singură dată.

Reuniunea mai multor mulțimi. Reuniunea unei familii de mulțimi se exprimă astfel: $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{pentru un anumit}\:\: i \in I \} $$

Cum se calculează reuniunea a două mulțimi

Să analizăm un exemplu practic al reuniunii dintre două mulțimi A și B.

Explicație. Mulțimea A conține elementele { 2, 5, 6, 7, 8 }, iar mulțimea B cuprinde { 1, 3, 4, 6, 7, 9 }. Reuniunea lor este { 1, 2, 3, 4, 5, 6, 7, 8, 9 }. Elementele comune {6, 7} apar o singură dată.

Intersecția

Intersecția a două mulțimi A și B este mulțimea elementelor pe care cele două mulțimi le au în comun.

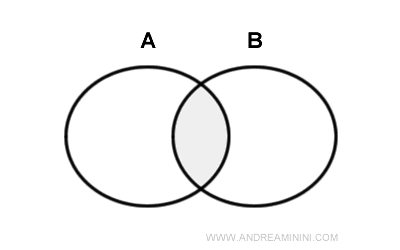
Simbolul intersecției este ⋂.

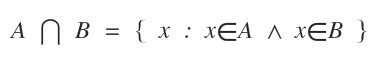
Două mulțimi A și B se numesc disjuncte dacă intersecția lor A⋂B este mulțimea vidă.

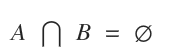
Intersecția mai multor mulțimi. Intersecția unei familii de mulțimi se notează astfel: $$ \bigcap_{i \in I} = \{ x \in A_i \:\: \forall i \in I \} $$

Cum se calculează intersecția a două mulțimi

Iată un exemplu concret de intersecție.

Explicație. Elementele { 6, 7 } se află atât în A, cât și în B, prin urmare intersecția A⋂B este { 6, 7 }.

Diferența dintre mulțimi

Diferența dintre două mulțimi A și B, notată A - B, este mulțimea elementelor care aparțin lui A, dar nu și lui B.

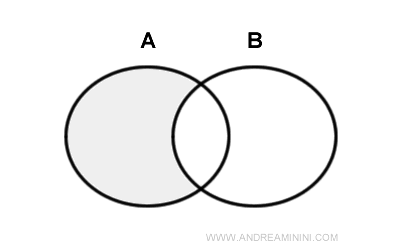
Această operație se mai numește și complementul lui B în raport cu A.

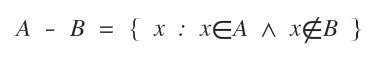
Notă. Diferența A - B se numește și complement relativ al lui A față de B. Ea conține toate elementele din A care nu apar în B. Se exprimă astfel: $$ A \text{ \ } B =\{ x \in A \mid x \notin B \} $$

Cum se calculează diferența a două mulțimi

Iată un exemplu concret pentru diferența A - B.

Explicație. Mulțimea A este {2, 5, 6, 7, 8}. Deoarece elementele {6, 7} apar și în B, acestea se elimină din A la calculul diferenței, rezultatul fiind {2, 5, 8}.

Proprietățile Operațiilor cu Mulțimi

Operațiile cu mulțimi respectă câteva proprietăți esențiale: comutativitatea, asociativitatea, distributivitatea și legile lui De Morgan.

• Proprietatea comutativă

  A ∪ B = B ∪ A
  A ∩ B = B ∩ A

• Proprietatea asociativă

  A ∪ (B ∪ C) = (A ∪ B) ∪ C
  A ∩ (B ∩ C) = (A ∩ B) ∩ C

• Proprietatea distributivă

  A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
  A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

• Legile lui De Morgan

  A - (B ∪ C) = (A - B) ∩ (A - C)
  A - (B ∩ C) = (A - B) ∪ (A - C)