Submulțimi improprii

Ce sunt submulțimile improprii?

Se numesc submulțimi improprii acele submulțimi care coincid cu mulțimea însăși sau cu mulțimea vidă.

Orice mulțime A are întotdeauna două submulțimi improprii:

• mulțimea identică cu ea însăși $$ A = A $$
• mulțimea vidă $$ Ø ⊂ A $$

Mulțimi egale

Presupunem că avem două mulțimi egale (A = B).

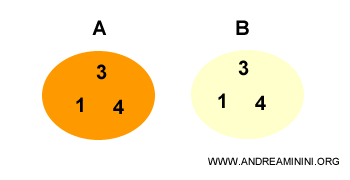
Fiecare element al lui A se găsește și în B, deci A este submulțime a lui B:

$$ A ⊆ B $$

În mod similar, fiecare element al lui B se găsește și în A, deci B este submulțime a lui A:

$$ B ⊆ A $$

Această incluziune reciprocă arată că cele două mulțimi sunt identice.

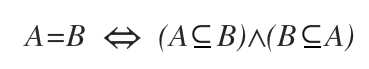
Astfel, când două mulțimi sunt egale (A = B), fiecare este submulțime a celeilalte.

În acest caz vorbim despre submulțimi improprii, deoarece nici A, nici B nu este submulțime proprie a celeilalte.

Notă: O mulțime A este submulțime proprie a lui B dacă toate elementele lui A aparțin lui B, iar B are cel puțin un element care nu aparține lui A. Această condiție nu este îndeplinită atunci când mulțimile sunt egale.

Exemplu

Mulțimea A este inclusă în B și invers:

$$ A = \{ 1,3,4 \} $$

$$ B = \{ 1,3,4 \} $$

Fiecare element al lui A se găsește în B și fiecare element al lui B se găsește în A.

Prin urmare, aceste două mulțimi sunt submulțimi improprii una față de cealaltă.

Mulțimea vidă

O mulțime se numește mulțime vidă dacă nu conține niciun element.

Se notează cu simbolul Ø: $$ Ø = \{ \ \ \} $$

Mulțimea vidă este o submulțime improprie a oricărei mulțimi.

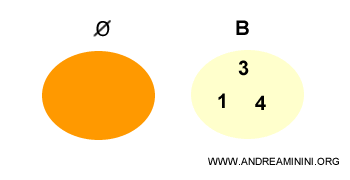
Notă: Faptul că mulțimea vidă este submulțime a oricărei mulțimi poate părea contraintuitiv, dar se demonstrează ușor (vezi demonstrația).

Exemplu

Considerăm mulțimea vidă și o mulțime A oarecare:

$$ Ø = \{ \ \ \} $$

$$ A = \{ 1,3,4 \} $$

Mulțimea vidă este inclusă în A:

$$ Ø ⊂ A $$

Pentru a demonstra acest fapt, presupunem contrariul și obținem o contradicție:

„Mulțimea vidă NU este submulțime a lui A”

Dacă aceasta ar fi adevărată, ar exista cel puțin un element în mulțimea vidă care să nu fie în A.

Dar acest lucru este imposibil, deoarece mulțimea vidă nu conține elemente.

Rezultă că afirmația „Mulțimea vidă NU este submulțime a lui A” este falsă.

Prin urmare, afirmația opusă - „Mulțimea vidă ESTE submulțime a lui A” - este adevărată.

Demonstrație alternativă: Reuniunea unei mulțimi A cu oricare dintre submulțimile sale B⊆A este întotdeauna egală cu A: $$ A \cup B = A $$ Aceeași proprietate este valabilă și pentru reuniunea cu mulțimea vidă: $$ A \cup Ø = \{ 1,3,4 \} \cup \{ \ \ \} = \{ 1,3,4 \} = A $$