Reuniunea Mulțimilor

Reuniunea a două mulțimi A și B este mulțimea alcătuită din toate elementele care se găsesc fie în A, fie în B, fie în ambele.

Simbolul utilizat pentru reuniune este ∪.

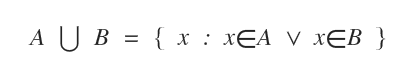
Se citește „reuniunea lui A și B” sau, mai simplu, A reuniune B.

Dacă există elemente comune celor două mulțimi, acestea apar o singură dată în reuniune.

Reuniunea mai multor mulțimi. Operația de reuniune se poate aplica și pentru o colecție de mai multe mulțimi. În acest caz, se folosește notația: $$ \bigcup_{i \in I} = \{ x \in A_i \:\: \text{pentru un anumit}\:\: i \in I \} $$

Exemplu practic

Să considerăm două mulțimi A și B.

Mulțimea A conține elementele { 2, 5, 6, 7, 8 }, iar mulțimea B cuprinde { 1, 3, 4, 6, 7, 9 }.

Reuniunea lui A și B se notează A ∪ B și este: { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.

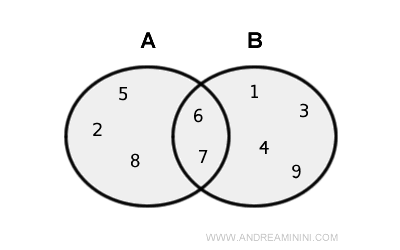
Notă. Elementele {6, 7} apar în ambele mulțimi. Totuși, în reuniunea A ∪ B, ele sunt incluse o singură dată, deoarece într-o mulțime nu există elemente duplicate.

Exemplul 2

Considerăm două mulțimi A și B:

$$ A = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

$$ B = \{ 2, 4, 6, 8 \} $$

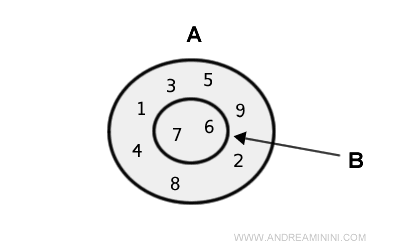
În acest caz, B este o submulțime proprie a lui A.

Prin urmare, reuniunea lor este chiar mulțimea A:

$$ A \cup B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

Elementele comune nu se dublează.

Exemplul 3

Acum să luăm mulțimile:

$$ A = \{ 1 , 3, 5, 7, 9 \} $$

$$ B = \{ 2, 4, 6, 8 \} $$

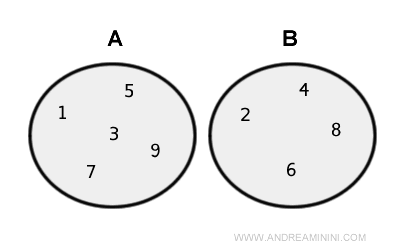
De această dată, mulțimile sunt disjuncte, adică nu au niciun element comun.

Reuniunea lor conține toate elementele din A și B:

$$ A \cup B = \{ 1 , 2, 3, 4, 5, 6, 7, 8, 9 \} $$

Imaginea următoare ilustrează reuniunea printr-o diagramă Euler-Venn.

Notă. Reuniunea mulțimilor corespunde disjuncției logice inclusive („OR”). Spre deosebire de disjuncția exclusivă (XOR), care exclude una dintre variante, reuniunea include toate elementele celor două mulțimi, inclusiv pe cele comune.

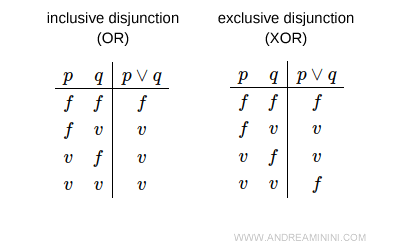
De aceea, când comparăm reuniunea cu disjuncția logică, trebuie specificat că este vorba despre disjuncția inclusivă.

Proprietățile Reuniunii

Reuniunea mulțimilor respectă o serie de proprietăți similare celor întâlnite la adunare și înmulțire în aritmetică:

• Proprietatea comutativă
  Ordinea mulțimilor nu influențează rezultatul: $$ A \cup B = B \cup A $$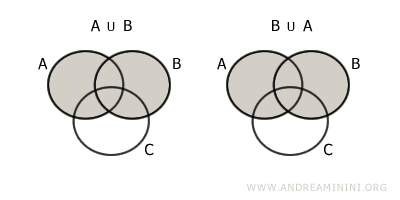

  

• Proprietatea asociativă
  Modul de grupare a mulțimilor nu modifică reuniunea: $$ (A \cup B) \cup C = A \cup (B \cup C) $$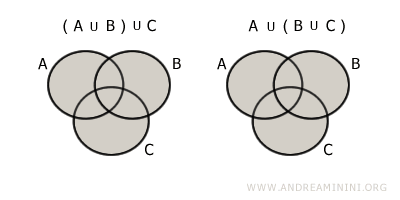

  

• Proprietatea distributivă a reuniunii față de intersecție
  Reuniunea unei mulțimi cu intersecția altor două este echivalentă cu intersecția reuniunilor:

  $$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$
  

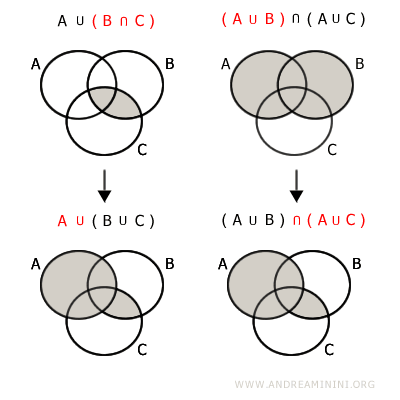
Cardinalitatea Reuniunii

Cardinalitatea reuniunii depinde de faptul dacă mulțimile au sau nu elemente comune.

• Mulțimi disjuncte
  Dacă nu există elemente comune, cardinalitatea reuniunii este suma cardinalităților fiecărei mulțimi: $$ |A\cup B|=|A| + |B| $$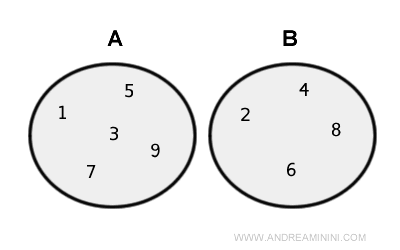

  

• Mulțimi cu elemente comune
  Când două mulțimi au elemente comune, cardinalitatea reuniunii se obține prin scăderea intersecției: $$ |A\cup B|=|A| + |B| - |A\cap B| $$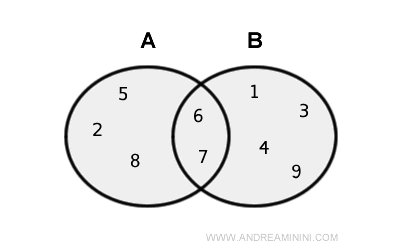

  

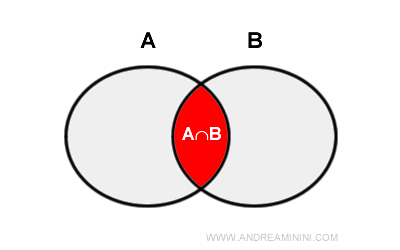
  Explicație. Dacă adunăm elementele celor două mulțimi, cele din intersecția A⋂B sunt numărate de două ori. Pentru a determina corect cardinalitatea lui A ∪ B, trebuie să scădem o dată aceste elemente, evitând astfel dublarea.

  

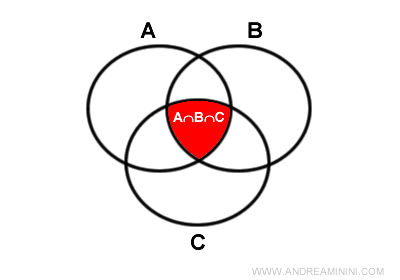
  Pentru trei mulțimi care nu sunt disjuncte, cardinalitatea reuniunii se calculează prin principiul incluziunii-excluziunii:

  $$ |A\cup B\cup C| = |A| + |B| + |C| - |A\cap B| - |A\cap C| - |B\cap C| + |A\cap B\cap C| $$

  Aici, intersecțiile dintre câte două mulțimi au fost adunate de două ori, de aceea trebuie scăzute. Însă intersecția celor trei mulțimi A⋂B⋂C a fost eliminată în exces, deci trebuie adăugată din nou pentru a corecta rezultatul.

  Explicație. În suma |A| + |B| + |C|, elementele din intersecțiile |A⋂B|, |A⋂C| și |B⋂C| sunt luate de două ori, iar cele din intersecția |A⋂B⋂C| de trei ori. Pentru a corecta, scădem o dată fiecare intersecție a câte două mulțimi. Procedând astfel, elementele din intersecția |A⋂B⋂C| dispar de trei ori, motiv pentru care trebuie adăugate înapoi o dată.
  

Acest principiu se aplică și pentru reuniunea unui număr mai mare de mulțimi, urmând aceeași regulă a incluziunii-excluziunii.