Mulțimi mărginite
Ce este o mulțime mărginită?
O mulțime se numește mărginită dacă există un număr real \( M \) astfel încât fiecare element al ei se află între \( -M \) și \( +M \). Cu alte cuvinte: $$ -M \leq a \leq M \quad \forall a \in A $$ sau, echivalent: $$ |a| \leq M \quad \forall a \in A $$
A fi mărginită înseamnă că mulțimea are atât o limită superioară, cât și una inferioară.
Demonstrație
A] Dacă pornim de la inegalitatea:
$$ |a| \leq M \quad \forall a \in A $$
Din definiția valorii absolute rezultă imediat:
$$ -M \leq a \leq M \quad \forall a \in A $$
Așadar, \( -M \) este o limită inferioară, iar \( +M \) este o limită superioară.
B] Dacă, dimpotrivă, presupunem că:
$$ l \leq a \leq L \quad \forall a \in A $$
unde \( l \) și \( L \) sunt numere reale, putem construi o limită generală alegând:
$$ M = \max(|l|, |L|) $$
Astfel obținem:
$$ |a| \leq M \quad \forall a \in A $$
care implică:
$$ -M \leq l \leq a \leq L \leq M \quad \forall a \in A $$
Exemplu practic
Să considerăm mulțimea realelor \( A \), alcătuită din următoarele șapte elemente:
$$ A = \{ -7, 4, 2, 6, 3, 5, 1 \} $$
A are o infinitate de limite inferioare în intervalul \( (-\infty, -7] \) și o infinitate de limite superioare în \( [6, +\infty) \).
Limitele „cele mai strânse” sunt: cea mai mare limită inferioară \( l = -7 \) și cea mai mică limită superioară \( L = 6 \).
$$ l = -7, \quad L = 6 $$
Apoi calculăm \( M \), valoarea absolută maximă dintre \( l \) și \( L \):
$$ M = \max(|l|, |L|) = \max(7,6) = 7 $$
Prin urmare, există un număr real \( M = 7 \) pentru care:
$$ -M \leq a \leq M \quad \forall a \in A $$
adică:
$$ -7 \leq a \leq 7 \quad \forall a \in A $$
Astfel, mulțimea \( A \) este într-adevăr mărginită.
Mulțimi mărginite inferior
O mulțime este mărginită inferior dacă există un număr real \( M \) astfel încât: $$ a \geq M \quad \forall a \in A $$
O astfel de mulțime are întotdeauna cel puțin o limită inferioară.
În acest caz, ea are un număr finit numit infim, adică cea mai mare dintre limitele inferioare.
Pentru o mulțime nevide și mărginită de numere reale, infimul este cea mai mare dintre toate limitele inferioare.
$$ m = \inf(A) = \begin{cases} m \leq a \quad \forall a \in A \\ \\ \forall \epsilon > 0, \: \exists a \in A \text{ astfel încât } m + \epsilon > a \end{cases} $$
Exemplu: Mulțimea numerelor reale pozitive \( R^+ \) este mărginită inferior, deoarece toate elementele se află în intervalul \( (0, +\infty) \). Infimul este \( M = 0 \), fiind cea mai mare limită inferioară. În schimb, nu este mărginită superior, întrucât nu are o limită finită, iar supremul este \( +\infty \).
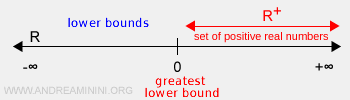
Dacă o mulțime nu este mărginită inferior, infimul ei este minus infinit (-∞):
$$ \inf(A) = -\infty \Leftrightarrow \forall l \in R, \: \exists a \in A \text{ astfel încât } a < l $$
Mulțimi mărginite superior
O mulțime este mărginită superior dacă există un număr real \( M \) astfel încât: $$ a \leq M \quad \forall a \in A $$
O asemenea mulțime are întotdeauna cel puțin o limită superioară.
În acest caz, ea are un număr finit numit suprem, adică cea mai mică dintre limitele superioare.
Pentru o mulțime nevide și mărginită de numere reale, supremul este cea mai mică dintre toate limitele superioare.
$$ M = \sup(A) = \begin{cases} M \geq a \quad \forall a \in A \\ \\ \forall \epsilon > 0, \: \exists a \in A \text{ astfel încât } M - \epsilon < a \end{cases} $$
Exemplu: Mulțimea numerelor reale negative \( R^- \) este mărginită superior, deoarece toate elementele se află în intervalul \( (-\infty, 0) \). Suprema este \( M = 0 \), fiind cea mai mică limită superioară. În schimb, nu este mărginită inferior, pentru că nu are o limită inferioară finită, iar infimul este \( -\infty \).
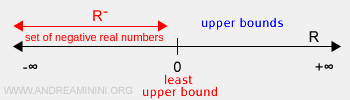
Dacă o mulțime nu este mărginită superior, supremul ei este infinitul pozitiv (+∞):
$$ \sup(A) = +\infty \Leftrightarrow \forall L \in R, \: \exists a \in A \text{ astfel încât } a > L $$
Mulțime mărginită în plan
O mulțime \(A \subseteq \mathbb{R}^2\) se numește mărginită în plan dacă există un număr real pozitiv \(M > 0\) și un punct \(P_0\) în plan, astfel încât pentru orice punct \(P \in A\) să avem distanța \(d(P, P_0) < M\). \[ \exists P_0 \in \mathbb{R}^2, \exists M > 0 \text{ astfel încât } \forall P \in A, \quad d(P, P_0) < M \] unde \(d(P, P_0)\) este distanța euclidiană.
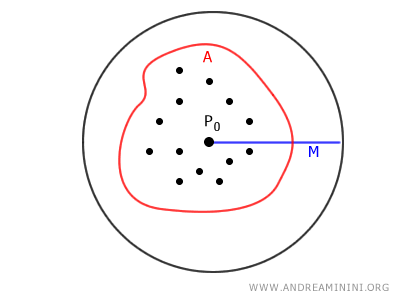
Cu alte cuvinte, o mulțime din \(\mathbb{R}^2\) este mărginită dacă toate punctele ei se află în interiorul unui cerc cu rază finită.
În general, o mulțime este mărginită dacă nu se întinde la infinit în nicio direcție și poate fi inclusă integral într-un cerc suficient de mare.
Exemple de mulțimi mărginite în plan sunt:
- Un cerc de rază \(r\), cu sau fără frontieră.
- Un pătrat, un dreptunghi, un triunghi sau orice alt poligon.
- Orice figură închisă cu dimensiuni finite.
Notă: În schimb, mulțimile nemărginite includ o dreaptă, o parabolă, o spirală care se extinde la infinit (de pildă \(y = x^2\)) sau un cadran întreg al planului cartezian.