Complementul unei Mulțimi

Dacă mulțimea B este o submulțime a lui A $$ B⊆A $$, complementul relativ al lui B în raport cu A este mulțimea alcătuită din toate elementele lui A care nu aparțin lui B: $$ A \text{ \ } B = \{ x \in A \;|\; x \notin B \} $$. Acesta mai este numit și complementul relativ al lui B în A.

Se citește: "mulțimea A\B este complementul mulțimii B" sau "A\B este complementul relativ al lui B în A".

Mai jos este prezentată diagrama Venn corespunzătoare.

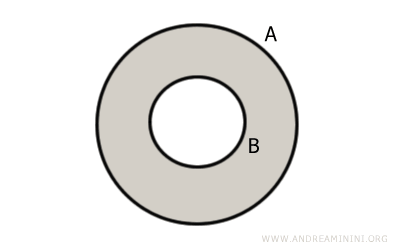
Zona gri reprezintă complementul lui B în A, adică mulțimea A\B.

Complementul coincide cu diferența dintre mulțimile A și B.

Un exemplu practic

Să analizăm un caz concret cu două mulțimi finite A și B:

$$ A = \{ 2, 4, 6, 8, 10 \} $$

$$ B = \{ 4, 6 \} $$

Complementul lui B în raport cu A este format din elementele lui A care nu aparțin lui B:

$$ A \text{ \ } B = A-B = \{ 2, 8, 10 \} $$

Reprezentarea grafică printr-o diagramă Euler - Venn este următoarea:

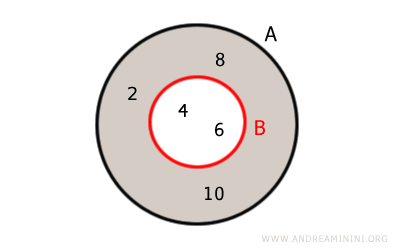
Explicație. Numerele 4 și 6 se găsesc atât în A, cât și în B, fiind elemente comune celor două mulțimi. În schimb, complementul lui B în A conține elementele lui A care nu se află în B, adică { 2, 8, 10 }.

Exemplul 2

Să considerăm acum două mulțimi infinite.

Mulțimea numerelor naturale \( N = \{1, 2, 3, 4, 5, ...\} \) și submulțimea numerelor naturale pare \( P = \{2, 4, 6, 8, ...\} \).

$$ N = \{ 1, 2, 3, 4, 5, ... \ \} $$

$$ P = \{ 2, 4, 6, 8, ... \ \} $$

Complementul lui P în raport cu N este mulțimea numerelor naturale impare \( D \):

$$ N \text{ \ } P = D = \{ 1, 3, 5, 7, 9, ... \ \} $$

Complementul absolut

Complementul absolut al unei mulțimi A față de mulțimea universală U este alcătuit din toate elementele din U care nu aparțin lui A: $$ C_A = \{ x \in U \;|\; x \notin A \} $$. Este cunoscut și sub denumirea de complementul absolut al lui A.

Ce este mulțimea universală?

Mulțimea universală \( U \) este acea mulțime care conține toate mulțimile luate în considerare într-un anumit context.

Dacă nu se precizează altfel, prin mulțime universală se înțelege mulțimea tuturor elementelor posibile din domeniul de studiu.

Exemplu

Să presupunem că avem o mulțime \( A \) inclusă în mulțimea universală \( U \).

Complementul lui \( A \), notat \( C_A \) (zona gri din diagramă), este format din toate elementele din \( U \) care nu aparțin lui \( A \) (zona albă).

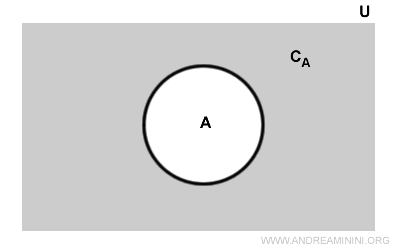
Se spune: "mulțimea U\A (sau U-A) este complementul mulțimii A".

Complementul \( U  \text{ \ }  A \) poate fi notat și \( U-A \), \( C_A \), \( A^C \) sau \( -A \).

Observații

Câteva proprietăți utile ale complementelor:

• Complementul lui A față de ea însăși este mulțimea vidă, deoarece \( A - A = Ø \).

  $$ A \text{ \ } A = A - A = Ø $$

• Dacă \( A \) și \( B \) sunt mulțimi egale (\( A = B \)), complementul lor este mulțimea vidă.

  $$ A = B \Longleftrightarrow A - B = Ø $$

• Complementul mulțimii vide față de \( A \) este chiar \( A \), deoarece \( A - Ø = A \).

  $$ Ø \text{ \ } A = A $$

• Uniunea lui \( A \) cu complementul lui \( A \) în raport cu \( B \) (adică \( B \setminus A \)) este mulțimea \( B \).

  $$ A \cup (B \text{ \ } A) = B $$

• Intersecția lui \( A \) cu complementul său față de \( B \) (adică \( B \setminus A \)) este mulțimea vidă.

  $$ A \cap (B \text{ \ } A) = Ø $$

Și așa mai departe.