Spațiu topologic normal
Un spațiu topologic \( X \) se numește normal atunci când îndeplinește două condiții esențiale:
- Orice singleț este o mulțime închisă
Adică pentru orice punct \( x \in X \), mulțimea \(\{x\}\) este închisă în topologia considerată. - Două mulțimi închise și disjuncte pot fi separate prin deschise disjuncte
Dacă \( A \) și \( B \) sunt închise și nu au puncte comune, există deschise \( U \) și \( V \) astfel încât:
- \( A \subset U \)
- \( B \subset V \)
- \( U \cap V = \emptyset \)
Pe scurt, un spațiu normal permite separarea elegantă a două mulțimi închise care nu se intersectează. Putem găsi deschise distincte care le conțin și nu se suprapun deloc. Această proprietate devine extrem de utilă atunci când vrem să construim funcții continue care disting puncte sau regiuni ale spațiului.
Exemplu concret
Să revenim la un exemplu familiar: spațiul \( \mathbb{R} \) cu topologia obișnuită, bazată pe intervalele deschise \( (a, b) \).
Alegem două mulțimi închise și disjuncte:
- \( A = \{0\} \), un singleț.
- \( B = [2, 3] \), un interval închis.
Aceste două mulțimi sunt închise în \( \mathbb{R} \), iar faptul că nu se ating le face disjuncte.
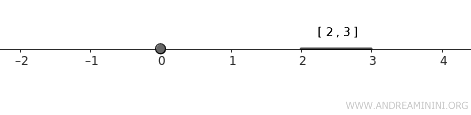
Observație. Singlețul \( A \) este închis deoarece are un singur element. Intervalul \( B \) este închis prin definiție.
Putem acum construi deschise care separă clar cele două mulțimi.
Pentru \( A \), alegem deschisul \( U = (-1, 1) \), suficient pentru a conține punctul \( 0 \).
$$ A \subset U = (-1,1) $$
Pentru \( B = [2,3] \), luăm deschisul \( V = (1, 4) \), care acoperă întreg intervalul.
$$ B \subset V = (1,4) $$
Deschisele \( U \) și \( V \) nu se intersectează, deci
$$ U \cap V = \emptyset $$
Acesta este exact tipul de separare cerut de normalitate.
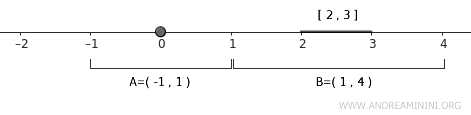
Aceeași idee funcționează pentru orice două mulțimi închise disjuncte. De aceea, \( \mathbb{R} \) cu topologia sa uzuală este un exemplu clasic de spațiu normal.
Observații suplimentare
Câteva lucruri importante de reținut despre spațiile normale:
- Dreapta reală \( \mathbb{R} \) este un spațiu normal
Ea satisface atât regularitatea, cât și condiția mai puternică de normalitate. - Orice spațiu metric este normal
Prezența unei metrici garantează normalitatea spațiului. Este un rezultat clasic în topologie. - Orice spațiu normal este regulat
Normalitatea implică regularitatea, dar inversul nu este întotdeauna adevărat.
Aceste proprietăți fac din spațiile normale un instrument important în înțelegerea structurii topologice a spațiilor și în construirea de funcții cu proprietăți bine controlate.