Baza unei Topologii
O bază a unei topologii este o colecție \( B \) de mulțimi deschise din care putem reconstrui toate deschisele unui spațiu topologic \( T \). Cu alte cuvinte, baza oferă elementele minimale din care se formează întreaga structură topologică.
Fie ansamblul \( X \), împreună cu o colecție \( T \) de submulțimi care îi definesc topologia. În acest cadru, o bază este o colecție \( B \) de mulțimi, numite mulțimi de bază, ce respectă două condiții esențiale:
- Fiecare element \( x \in X \) trebuie să se afle în cel puțin o mulțime din \( B \).
- Dacă un punct \( x \) aparține intersecției \( B_1 \cap B_2 \), unde \( B_1, B_2 \in B \), atunci există o mulțime \( B_3 \in B \) cu \( x \in B_3 \subseteq B_1 \cap B_2 \). Aceasta garantează că baza este suficient de „fină" pentru a descrie local orice punct.
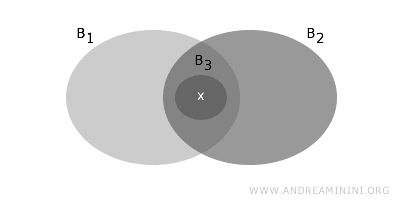
Aceste două proprietăți asigură că baza generează topologia în mod coerent și complet.
De ce este importantă o bază?
Într-o topologie pot exista foarte multe mulțimi deschise. În loc să le enumerăm pe toate, o bază permite descrierea întregii topologii folosind un set mai mic de mulțimi generatoare. Este o metodă eficientă de organizare și înțelegere a structurii topologice, utilă atât în studiul teoretic, cât și în aplicații.
Observație: Condiția privind intersecțiile este crucială, deoarece garantează respectarea axiomei conform căreia intersecția a două deschise este un deschis.
Un exemplu simplu
Considerăm ansamblul
$$ X = \{a, b, c \} $$
cu topologia
$$ T = \{ \emptyset, \{ a \}, \{ b,c \}, \{ a,b,c \} \} $$
O bază posibilă este:
$$ B = \{ \{ a \}, \{ b,c \} \} $$
De ce funcționează această bază? Pentru că fiecare element al lui \( X \) se regăsește într-o mulțime de bază, iar toate deschisele se obțin ca reuniuni de elemente din \( B \).
Exemple:
- \( \{a\} \) este deja în \( B \).
- \( \{b,c\} \) este în \( B \).
- \( \{a,b,c\} = \{a\} \cup \{b,c\} \).
Observație: Mulțimea vidă este mereu un deschis și apare în orice topologie, indiferent de baza folosită. $$ \emptyset \in T $$
Acest exemplu arată clar cum se construiește o bază într-un caz finit. Pe ansambluri mai mari, mecanismul este același, doar că numărul mulțimilor poate crește considerabil.
O altă modalitate de a construi o bază
O bază alternativă pentru același ansamblu este:
$$ B = \{ \{ a \}, \{ b \}, \{ c \} \} $$
Aici baza este formată din singletoane, adică mulțimi cu un singur element.
Verificăm că această colecție generează aceeași topologie:
- \( \varnothing \) este deschis.
- \( \{a\} \) este un element al bazei.
- \( \{b,c\} = \{b\} \cup \{c\} \).
- \( X = \{a\} \cup \{b\} \cup \{c\} \).
În concluzie, baza este validă și generează toate deschisele prin reuniune.
Observație: O topologie poate avea mai multe baze. Alegerea uneia sau alteia depinde de nivelul de detaliu dorit sau de contextul matematic.
Exemplul 2: cazul numerelor reale
Topologia standard pe \( \mathbb{R} \) are ca bază mulțimea tuturor intervalelor deschise:
$$ B = \{ (a,b) \subseteq \mathbb{R} \mid a < b \} $$
Orice punct din \( \mathbb{R} \) aparține unui interval deschis, iar intersecția a două intervale deschise care conțin același punct include întotdeauna un subinterval deschis.
De exemplu, intersecția intervalelor \( (0,3) \) și \( (2,4) \) este \( (2,3) \):
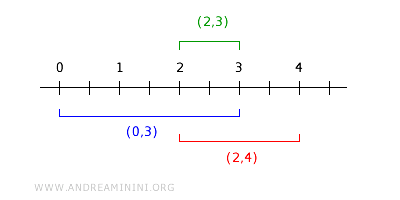
Rezultatul: $$ (0,3) \cap (2,4) = (2,3) \in B $$ ceea ce confirmă că baza este stabilă la intersecții.
Observații suplimentare
Bazele topologice permit construirea diferitelor tipuri de topologii pe același ansamblu. De exemplu, dacă baza conține toate singletoanele:
Dacă \( B = \{ \{x\} \mid x \in X \} \), atunci reunind aceste singletoane putem genera topologii foarte diverse.
De exemplu, pentru \( X = \{a,b,c\} \), aceeași bază poate genera topologii diferite:
- \( T = \{ \varnothing, \{b\}, \{a,c\}, X \} \)
- topologia trivială \( T = \{ \varnothing, X \} \)
- topologia discretă cu toate submulțimile posibile
Observație: Condițiile unei baze sunt automat îndeplinite, deoarece fiecare punct este acoperit de un singleton, iar singletoanele sunt disjuncte.
În general, principiul bazelor se aplică oricărui ansamblu, finit sau infinit, și oricărei topologii generate prin reuniuni ale elementelor bazei.