Închiderea unei mulțimi
Închiderea unei mulțimi \( A \) într-un spațiu topologic \( X \) este intersecția tuturor mulțimilor închise care conțin mulțimea \( A \). Această intersecție se notează cu \( \text{Cl}(A) \).
Intuitiv, închiderea lui \( A \) este cea mai mică mulțime închisă care o conține complet. Nu există o mulțime închisă mai mică ce ar putea include toate elementele lui \( A \).
Observație: Această proprietate rezultă direct din definiție. Închiderea este obținută ca intersecție a tuturor mulțimilor închise care conțin pe \( A \), deci reprezintă „limita minimă” a acestora.
Formal, închiderea lui \( A \) este definită prin relația:
$$ \text{Cl}(A) = \bigcap \{ C \subseteq X \mid A \subseteq C \text{ și } C \text{ este închisă în } X \} $$
Aici, \( \text{Cl}(A) \) reprezintă închiderea mulțimii \( A \), iar simbolul \( \bigcap \) indică intersecția tuturor mulțimilor închise care o conțin.
Închiderea lui \( A \) cuprinde atât elementele lui \( A \), cât și toate punctele sale de acumulare din spațiul \( X \).
Observație: Închiderea unei mulțimi depinde esențial de topologia spațiului în care este definită. Aceeași mulțime poate avea închideri diferite în topologii diferite.
Un exemplu ilustrativ
Să considerăm mulțimea \( A = (0, 1) \) din \( \mathbb{R} \), echipată cu topologia uzuală.
Este vorba despre intervalul deschis format din toate numerele reale strict cuprinse între 0 și 1.
În acest caz, închiderea lui \( A \) este:
$$ \text{Cl}(A) = [0,1] $$
Această mulțime conține intervalul inițial \( (0,1) \), precum și punctele de acumulare 0 și 1.
Observație: În topologia uzuală pe \( \mathbb{R} \), o mulțime este închisă dacă și numai dacă include toate punctele sale de acumulare. Un punct este de acumulare dacă orice vecinătate a sa conține cel puțin un punct al mulțimii. De exemplu, intersecția intervalelor închise [0,2] și [-1,1] este [0,1]. $$ [0,2] \cap [-1,1] = [0,1] $$
Exemplul 2
Să analizăm mulțimea \( A = [0,1) \) din \( \mathbb{R} \), considerată tot cu topologia uzuală.
Este un interval închis la stânga și deschis la dreapta, care conține toate valorile reale cuprinse între 0 și 1, cu excepția lui 1.
Și în acest caz, închiderea este:
$$ \text{Cl}(A) = [0,1] $$
Punctul 0 aparține deja mulțimii, iar 1 este un punct de acumulare exterior. Prin urmare, închiderea adaugă doar capătul drept.
Observație: Acest exemplu evidențiază clar rolul punctelor de acumulare în definirea închiderii unei mulțimi.
Exemplul 3
Să considerăm acum aceeași mulțime \( A = [0,1) \), dar într-un spațiu \( X \) prevăzut cu topologia discretă.
În această topologie, orice submulțime este simultan deschisă și închisă.
- Mulțime deschisă
Orice submulțime a lui \( X \) este deschisă. - Mulțime închisă
Orice submulțime este și închisă, deoarece complementul său este deschis.
Prin urmare, orice mulțime este clopen, adică simultan deschisă și închisă.
În acest context, închiderea lui \( A \) coincide exact cu \( A \), deoarece aceasta este deja o mulțime închisă.
$$ \text{Cl}(A) = [0,1) $$
Observație: Acest exemplu arată cât de mult influențează topologia rezultatul final. Noțiunea de închidere nu depinde doar de mulțime, ci în mod esențial de structura topologică a spațiului.
Exemplul 4
Să considerăm un spațiu topologic \( X = \{a, b, c\} \), echipat cu topologia discretă.
În acest caz, orice submulțime este deschisă:
- \( \emptyset \) și \( \{a, b, c\} \) sunt deschise prin definiție.
- Mulțimile \( \{a\} \), \( \{b\} \), \( \{c\} \) sunt deschise.
- Orice combinație, precum \( \{a, b\} \), \( \{a, c\} \) sau \( \{b, c\} \), este de asemenea deschisă.
Deoarece complementul oricărei submulțimi este tot o mulțime deschisă, rezultă că toate submulțimile sunt simultan deschise și închise.
Dacă alegem \( A = \{b, c\} \), observăm că aceasta este atât deschisă, cât și închisă.
Închiderea lui \( A \), notată \( \text{Cl}(A) \), este intersecția tuturor mulțimilor închise care conțin \( A \). În acest caz, nu este necesară adăugarea niciunui element.
Rezultă astfel:
\[ \text{Cl}(A) = \{b, c\} \]
Într-o topologie discretă, fiecare mulțime este deja închisă, astfel încât închiderea coincide întotdeauna cu mulțimea inițială.
Observație: Pentru confirmare, observăm că mulțimile închise care conțin pe \( A \) sunt \( \{b, c\} \) și \( \{a, b, c\} \). Intersecția lor este $$ \text{Cl}(A) = \{b, c\} \cap \{a, b, c\} = \{b, c\}. $$ Prin urmare, închiderea lui \( A \) coincide exact cu \( A \).
Teorema închiderii unei mulțimi
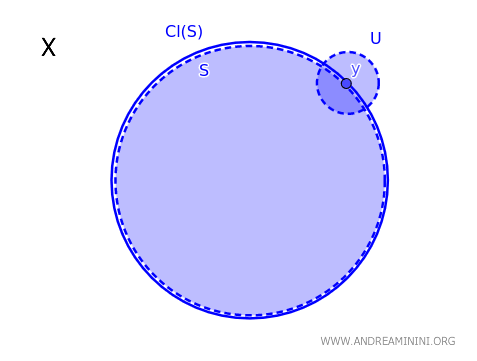
Într-un spațiu topologic \( X \), un punct \( y \) aparține închiderii unei submulțimi \( S \), notată \( \text{Cl}(S) \), dacă și numai dacă orice mulțime deschisă \( U \) care îl conține pe \( y \) intersectează mulțimea \( S \). Formal: \( y \in \text{Cl}(S) \iff \forall\, U \text{ deschis cu } y \in U,\; U \cap S \neq \varnothing \).
Cu alte cuvinte, un punct aparține închiderii unei mulțimi atunci când nu poate fi „separat” de aceasta prin niciun vecinătate deschisă.
Această formulare oferă un criteriu clar și foarte util pentru a stabili dacă un punct aparține închiderii unei mulțimi într-un spațiu topologic.
Demonstrație
- Condiție necesară
Dacă \( y \in \text{Cl}(S) \), atunci, prin definiție, orice mulțime deschisă care îl conține pe \( y \) trebuie să intersecteze mulțimea \( S \). Acest lucru se datorează faptului că închiderea cuprinde atât punctele lui \( S \), cât și punctele sale de acumulare. Un punct de acumulare este un punct pentru care orice vecinătate conține cel puțin un punct din \( S \), indiferent dacă acesta coincide sau nu cu punctul respectiv. - Condiție suficientă
Invers, dacă orice mulțime deschisă care conține punctul \( y \) intersectează mulțimea \( S \), atunci \( y \) este fie un element al lui \( S \), fie un punct de acumulare al acesteia. În ambele situații rezultă că \( y \in \text{Cl}(S) \).
Observație: Teorema exprimă o legătură profundă între noțiunea de deschidere și structura închiderii. Ea este fundamentală pentru studiul continuității, al convergenței și, în general, pentru analiza topologică.
Exemplu
Considerăm mulțimea \( A = (0, 2) \), definită în spațiul \( \mathbb{R} \) echipat cu topologia uzuală.
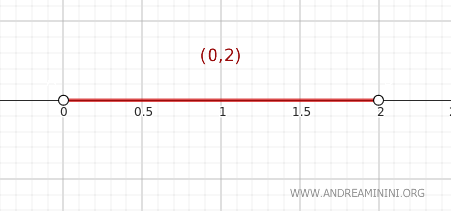
Aplicăm criteriul de mai sus pentru a verifica dacă un punct \( y \) aparține închiderii lui \( A \).
Să alegem punctul \( y = 2 \).
Conform definiției, \( y \in \text{Cl}(A) \) dacă și numai dacă orice vecinătate deschisă a lui \( y \) intersectează mulțimea \( A \).
- Analiza vecinătăților lui \( y \)
Orice interval deschis care conține punctul \( 2 \), de exemplu \( (1{,}9, 2{,}1) \), \( (1{,}95, 2{,}05) \) sau \( (1{,}99, 2{,}01) \), conține în mod necesar puncte din intervalul \( (0,2) \), precum \( 1{,}95 \) sau \( 1{,}99 \). - Verificarea condiției
Deoarece orice vecinătate a lui \( 2 \) intersectează mulțimea \( A \), rezultă că \( 2 \in \text{Cl}(A) \).
Prin urmare, punctul \( y = 2 \) aparține închiderii mulțimii \( A \), întrucât nu există nicio vecinătate a sa care să fie complet disjunctă de \( A \).
$$ y \in \text{Cl}(A) $$
Rezultă astfel că închiderea mulțimii \( A \) este intervalul închis \( \text{Cl}(A) = [0, 2] \), care conține explicit punctul \( y = 2 \).
Proprietăți ale închiderii în spații topologice
Mai jos sunt prezentate câteva proprietăți fundamentale ale operatorului de închidere, utile pentru înțelegerea structurii spațiilor topologice.
- Interiorul complementului și complementul închiderii
Interiorul complementului unei mulțimi \( A \) coincide cu complementul închiderii sale: $$ \operatorname{Int}(X \setminus A) = X \setminus \operatorname{Cl}(A) $$ - Închiderea complementului și complementul interiorului
Închiderea complementului lui \( A \) este complementul interiorului lui \( A \): $$ \operatorname{Cl}(X \setminus A) = X \setminus \operatorname{Int}(A) $$
Observații esențiale
Următoarele proprietăți rezumă comportamentul fundamental al operatorului de închidere:
- Dacă \( C \) este închis și \( A \subseteq C \), atunci \( \text{Cl}(A) \subseteq C \)
Deoarece \( \text{Cl}(A) \) este cea mai mică mulțime închisă care conține pe \( A \), ea este inclusă în orice mulțime închisă ce conține pe \( A \). - Dacă \( A \subseteq B \), atunci \( \text{Cl}(A) \subseteq \text{Cl}(B) \)
Operatorul de închidere este monoton: dacă o mulțime este inclusă în alta, aceeași relație se păstrează după aplicarea închiderii. - O mulțime este închisă dacă și numai dacă este egală cu propria sa închidere
O mulțime este închisă exact atunci când coincide cu închiderea sa. - Închiderea unei mulțimi este reuniunea acesteia cu mulțimea punctelor sale de acumulare
Dacă notăm cu \( A' \) mulțimea punctelor de acumulare ale lui \( A \), atunci: $$ \text{Cl}(A) = A \cup A' $$ - Idempotența operatorului de închidere
Aplicarea repetată a operatorului de închidere nu modifică rezultatul: $$ \text{Cl}(\text{Cl}(A)) = \text{Cl}(A) $$ - Incluziunea mulțimii inițiale
Orice mulțime este inclusă în propria sa închidere: $$ A \subseteq \text{Cl}(A) $$
Aceste proprietăți stau la baza teoriei topologice moderne și sunt esențiale pentru înțelegerea structurii și comportamentului spațiilor topologice.