Spații regulate în topologie
Un spațiu topologic \( X \) se numește regulat dacă respectă două cerințe esențiale:
- Orice singleton este închis, ceea ce înseamnă că fiecare punct din \( X \) formează o mulțime închisă.
- Un punct poate fi separat de o mulțime închisă: dacă \( a \in X \) și \( C \subset X \) este o mulțime închisă care nu îl conține, atunci există două mulțimi deschise disjuncte \( U \) și \( V \) cu: \[ a \in U, \quad C \subset V, \quad U \cap V = \emptyset \]
Regularitatea oferă un nivel mai fin de separare decât condiția Hausdorff. Ea arată cât de bine poate un spațiu să distingă puncte și submulțimi folosind deschise adecvate.
Mai mult, dacă un spațiu regulat are o bază numărabilă, teorema lui Urysohn garantează că spațiul este metrizabil, ceea ce îl apropie de intuițiile geometrice obișnuite.
În ce se deosebește de spațiile Hausdorff?
În spațiile Hausdorff ne interesează separarea oricăror două puncte diferite. În schimb, într-un spațiu regulat cerem ceva suplimentar: să putem separa și un punct de o mulțime închisă care nu îl conține. Aceasta este o cerință mai puternică și oferă o imagine mai clară asupra structurii locale a spațiului.
Observație. Nu orice spațiu regulat este și normal. Spațiile normale impun o condiție mai strictă: orice două mulțimi închise disjuncte trebuie separate prin mulțimi deschise disjuncte. Avem astfel o ierarhie: normal implică regulat, dar nu și invers.
Regularitatea este doar una dintre proprietățile de separare studiate în topologia generală. Există spații regulate care nu sunt Hausdorff, dar și spații Hausdorff care nu sunt regulate. Acest lucru arată că aceste condiții nu trebuie interpretate ca trepte ale aceleiași scară, ci ca proprietăți independente.
Un exemplu concret
Un exemplu accesibil de spațiu regulat este axa reală \( \mathbb{R} \), cu topologia standard pe care o cunoaștem din analiză.
Să luăm un punct \( x = 2 \) și o mulțime închisă care nu îl conține:
\[ C = (-\infty, 0] \cup [5, \infty) \]
Această mulțime este închisă, iar punctul nostru nu face parte din ea.

Pentru a demonstra regularitatea, trebuie să găsim două mulțimi deschise disjuncte, una care să conțină punctul \( x \), cealaltă mulțimea \( C \).
Complementul lui \( C \) este o mulțime deschisă, iar în interiorul său găsim ușor un interval deschis care cuprinde punctul:
\[ (0, 5) \]
Alegem apoi două numere reale astfel încât:
\[ 0 < c < 2 < d < 5 \]
O alegere simplă este \( c = 1 \) și \( d = 3 \).
Definim:
- \( U = (1, 3) \), deschisul care conține punctul nostru.
- \( V = (-\infty, 1) \cup (3, \infty) \), care conține mulțimea \( C \).
Aceste două deschise nu se intersectează, ceea ce confirmă separarea cerută.
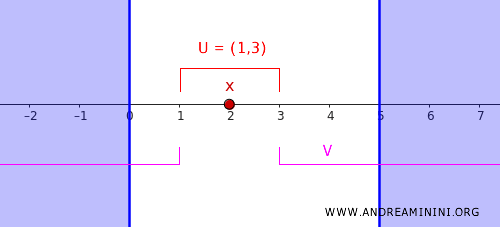
Am reușit astfel să ilustrăm direct definiția: axa reală, în topologia sa obișnuită, este un spațiu regulat.
Note
Idei utile pentru a fixa conceptul de spațiu regulat:
- Axiomele de separare
În topologia generală, proprietăți precum Hausdorff și regulat fac parte dintr-un sistem mai larg de criterii care descriu cât de eficient poate un spațiu să distingă puncte și submulțimi prin vecinătăți deschise. Aceste axiome ne ajută să înțelegem cât de „clară" este structura unui spațiu.Observație. Un spațiu este Hausdorff dacă două puncte diferite pot fi plasate în deschise care nu se ating. Este regulat dacă același tip de separare este posibil între un punct și o mulțime închisă care nu îl conține. Putem privi această idee ca pe o formă de „rezoluție topologică": cu cât este mai mare, cu atât spațiul distinge mai fin structurile locale.
Conceptul poate fi extins mult mai departe, dar acestea sunt ideile de bază pentru a înțelege și recunoaște spațiile regulate.