Frontiera unei mulțimi

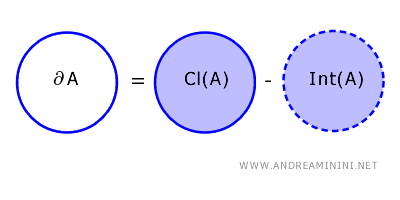
Frontiera unei mulțimi $ A $ dintr-un spațiu topologic $ X $ este formată din punctele care aparțin aderenței lui $ A $, dar nu se află în interiorul acesteia : \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

Intuitiv, frontiera descrie „linia de separație” dintre o mulțime și exteriorul ei. Este zona de contact în care nu ne aflăm nici complet în interior, nici complet în exterior.

Prin $ \text{Cl}(A) $ înțelegem aderența lui $ A $, adică mulțimea care conține toate punctele lui $ A $ împreună cu punctele sale limită.

În schimb, $ \text{Int}(A) $ reprezintă interiorul lui $ A $, adică totalitatea punctelor pentru care există un vecinaj deschis aflat integral în $ A $.

ilustrare a frontierei unei mulțimi într-un spațiu topologic

Este important de reținut că frontiera depinde de topologia aleasă. Aceeași mulțime poate avea o frontieră diferită dacă schimbăm structura topologică a spațiului.

Altfel spus, un punct aparține frontierei lui $ A $ dacă este „aproape” atât de puncte din $ A $, cât și de puncte din complementara sa $ X \setminus A $.

Un exemplu concret
Teorema frontierei
Observații

Un exemplu concret

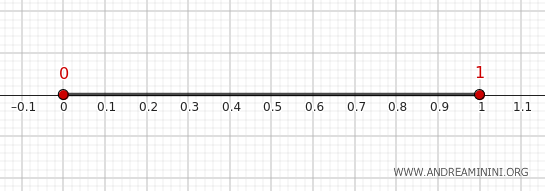
Considerăm mulțimea $ A = (0, 1) $, privită ca submulțime a dreptei reale $ \mathbb{R} $, dotată cu topologia uzuală.

Vom determina frontiera acestei mulțimi pas cu pas.

1] Aderența lui A

Aderența lui $ A $, notată $ \text{Cl}(A) $, cuprinde toate punctele intervalului deschis, precum și punctele sale limită.

În acest caz, punctele 0 și 1 sunt limite ale intervalului $ (0,1) $. Prin urmare:

$$ \text{Cl}(A) = [0, 1] $$

2] Interiorul lui A

Interiorul lui $ A $, notat $ \text{Int}(A) $, este format din punctele care admit un vecinaj complet inclus în $ A $.

Deoarece $ (0,1) $ este deja un interval deschis, interiorul coincide cu mulțimea însăși:

$$ \text{Int}(A) = (0, 1) $$

3] Frontiera lui A

Frontiera se obține eliminând interiorul din aderență:

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

Înlocuind expresiile obținute:

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

Așadar, în topologia uzuală a lui $ \mathbb{R} $, frontiera intervalului deschis $ (0,1) $ este formată din punctele 0 și 1.

Aceste puncte se află exact „pe margine”. Orice vecinaj al lor conține atât puncte din interiorul intervalului, cât și puncte din exterior.

frontiera intervalului (0,1) pe axa reală

Teorema frontierei

Un punct $ x \in X $ aparține frontierei $ \partial A $ a unei submulțimi $ A $ dacă și numai dacă orice vecinaj al lui $ x $ intersectează atât $ A $, cât și complementara sa $ X - A $.

Această afirmație oferă un criteriu practic și ușor de verificat pentru a stabili dacă un punct este sau nu un punct de frontieră.

Exemplu

Revenim la mulțimea $ A = (0, 1) \subset \mathbb{R} $.

Știm deja că:

$$ \text{Cl}(A) = [0, 1] \quad \text{și} \quad \text{Int}(A) = (0, 1) $$

Prin urmare:

$$ \partial A = \{0, 1\} $$

Să verificăm direct condiția teoremei.

1] Punctul 0

Orice vecinaj al lui 0, de forma $ (0-\epsilon, 0+\epsilon) $, cu $ \epsilon > 0 $, conține puncte din intervalul $ (0,1) $, dar și puncte din exteriorul acestuia.

Rezultă că $ 0 $ aparține frontierei.

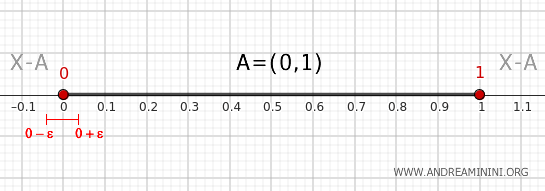
vecinaj al punctului 0 care intersectează mulțimea și exteriorul

2] Punctul 1

Situația este analogă pentru orice vecinaj al lui 1, care intersectează atât intervalul $ (0,1) $, cât și exteriorul acestuia.

Prin urmare, $ 1 \in \partial A $.

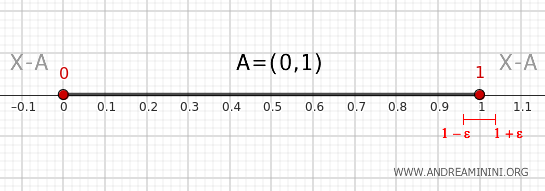
vecinaj al punctului 1 care intersectează mulțimea și exteriorul

3] Un punct interior

Alegem un punct din interiorul intervalului, de exemplu 0,5.

Orice vecinaj al acestui punct este complet inclus în $ A $ și nu intersectează complementara.

Prin urmare, 0,5 nu este punct de frontieră.

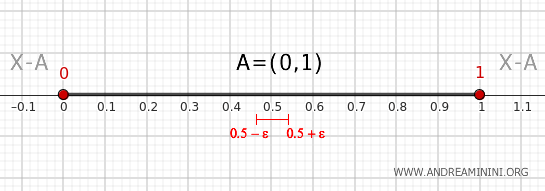
vecinaj al punctului 0,5 complet inclus în mulțime

Concluzia este clară: pentru intervalul $ (0,1) $, frontiera este formată exclusiv din punctele 0 și 1.

Observații

În încheiere, prezentăm câteva proprietăți utile ale frontierei în topologie:

Frontiera $ \partial A $ este inclusă în $ A $ dacă și numai dacă $ A $ este închisă.
Frontiera și mulțimea sunt disjuncte dacă și numai dacă $ A $ este deschisă.
Frontiera este vidă exact atunci când $ A $ este simultan deschisă și închisă (clopen).
Frontiera este intersecția aderenței lui $ A $ cu aderența complementarei sale.
Frontiera unei mulțimi este întotdeauna o mulțime închisă.
Frontiera și interiorul unei mulțimi nu au puncte comune.
Reuniunea dintre interior și frontieră coincide cu aderența mulțimii.

Aceste rezultate oferă un cadru clar pentru înțelegerea noțiunii de frontieră și a rolului său fundamental în topologie.