Caracterizarea frontierei unei mulțimi
Un punct \( x \) aparține frontierei unei mulțimi \( A \) dacă, pentru orice vecinătate a lui \( x \), apar atât puncte din \( A \), cât și puncte din complementul său \( X - A \).
Spus mai simplu, un punct se află pe frontieră atunci când nu putem găsi nicio vecinătate a sa care să fie inclusă complet nici în \( A \), nici în exteriorul lui. În orice direcție ne-am uita în jurul lui \( x \), întâlnim simultan puncte din interior și din exterior.
Un exemplu ilustrativ
Pentru a înțelege mai bine această idee, este util să analizăm un exemplu concret.
Considerăm mulțimea \( A = (0, 1) \), definită pe dreapta reală \( \mathbb{R} \).
Punctele 0 și 1 sunt puncte de frontieră ale lui \( A \). Motivul este că orice vecinătate a acestor puncte conține inevitabil valori din intervalul \( (0, 1) \), dar și valori din afara lui.
- Punctul 1
Orice vecinătate de forma \( (1 - \epsilon, 1 + \epsilon) \), cu ε ales oricât de mic, cuprinde o porțiune \( (1 - \epsilon, 1) \) aflată în \( A \) și o porțiune \( (1, 1 + \epsilon) \) situată în complement. De aceea, punctul 1 aparține frontierei lui \( A \).
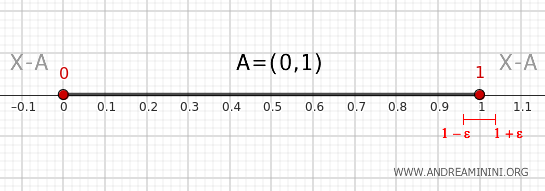
- Punctul 0
Situația este complet analogă pentru punctul 0. Orice vecinătate \( (0 - \epsilon, 0 + \epsilon) \) conține atât o parte \( (0, 0 + \epsilon) \) inclusă în \( A \), cât și o parte \( (0 - \epsilon, 0) \) aflată în complement. Prin urmare, și punctul 0 este un punct de frontieră al lui \( A \).
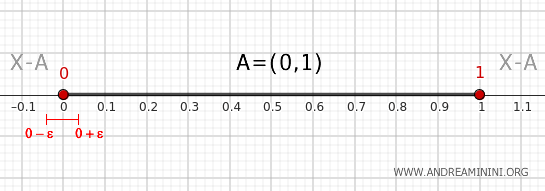
- Punct interior intervalului (0, 1)
Orice punct \( x \) strict cuprins între 0 și 1 are o vecinătate \( (x - \epsilon, x + \epsilon) \), cu ε > 0, care este inclusă în totalitate în \( A \). În acest caz, vecinătatea nu intersectează complementul, iar punctul respectiv nu se află pe frontieră.
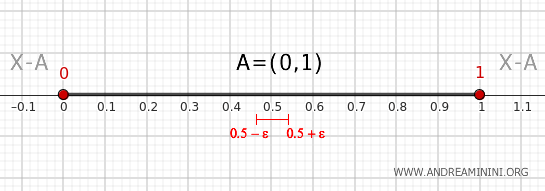
- Punct exterior intervalului (0, 1)
Orice punct situat strict în afara intervalului \( (0, 1) \), cu excepția extremelor 0 și 1, admite o vecinătate \( (x - \epsilon, x + \epsilon) \) complet inclusă în \( X - A \), fără nicio intersecție cu \( A \). Aceste puncte nu fac parte din frontieră.
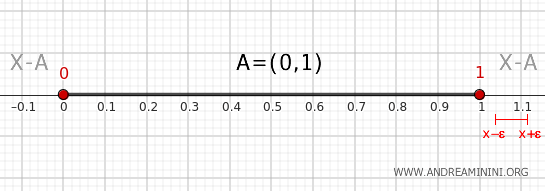
Prin urmare, singurele puncte de frontieră ale mulțimii \( A \) sunt 0 și 1:
$$ \partial A = \{0,1\} $$
În esență, un punct \( x \) aparține frontierei lui \( A \) dacă orice vecinătate a sa „atinge" atât interiorul, cât și exteriorul mulțimii. Acest criteriu oferă o modalitate clară și eficientă de identificare a punctelor de frontieră.
Demonstrația
Pentru a justifica formal această caracterizare, analizăm cele două implicații care o definesc.
1] Presupunem că \( x \in \partial A \
Conform definiției frontierei, această ipoteză este echivalentă cu relațiile:
$$ x \in \text{Cl}(A) \quad \text{și} \quad x \notin \text{Int}(A) $$
Faptul că \( x \in \text{Cl}(A) \) înseamnă că orice vecinătate a lui \( x \) intersectează mulțimea \( A \).
În același timp, condiția \( x \notin \text{Int}(A) \) arată că nicio vecinătate a lui \( x \) nu este inclusă complet în \( A \). Prin urmare, fiecare vecinătate conține în mod necesar puncte din complementul \( X - A \).
Rezultă astfel că orice vecinătate a lui \( x \) intersectează simultan mulțimea \( A \) și complementul său.
2] Presupunem că orice vecinătate a lui \( x \) intersectează atât \( A \), cât și \( X - A \)
Din această ipoteză rezultă imediat că \( x \in \text{Cl}(A) \) și \( x \in \text{Cl}(X - A) \).
Dar, deoarece \( \text{Cl}(X - A) = X - \text{Int}(A) \), deducem că \( x \notin \text{Int}(A) \).
În concluzie, avem:
$$ x \in \text{Cl}(A) \setminus \text{Int}(A) = \partial A $$
Reciproca este astfel demonstrată, iar caracterizarea frontierei unei mulțimi este complet justificată.