Conjuntos que não são nem abertos nem fechados 

Em topologia, um conjunto que não é nem aberto nem fechado não atende aos critérios necessários para se enquadrar em nenhuma dessas duas categorias.

Esse tipo de situação pode surgir em uma topologia onde o conjunto em questão não está definido como conjunto aberto, nem coincide com o complemento de um conjunto aberto.

Por isso, tal conjunto também não pode ser classificado como conjunto fechado.

Observação: Na topologia usual dos números reais, pode ser pouco intuitivo visualizar conjuntos que não sejam nem abertos nem fechados. No entanto, em estruturas topológicas mais gerais, a existência deles é perfeitamente natural. Um exemplo concreto ajuda a tornar esse conceito mais claro.

Exemplo prático

Considere o conjunto \( X = \{a,b,c,d\} \) e uma topologia \( T \) que define os seguintes conjuntos abertos: \( \{b\} \), \( \{a,b\} \), \( \{c,d\} \), \( \{b,c,d\} \), \( \{a,b,c,d\} \) e o conjunto vazio (Ø).

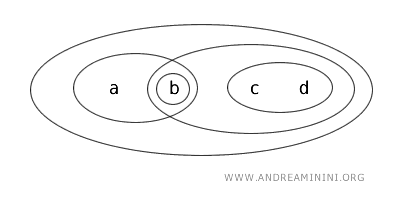
Vamos analisar agora o subconjunto \( \{b,c\} \) de \( X \).

• O conjunto \( \{b,c\} \) não é aberto na topologia \( T \), já que não aparece explicitamente na lista de conjuntos abertos.
• Por outro lado, \( \{b,c\} \) também não é fechado, pois o seu complemento \( X \setminus \{b,c\} = \{a,d\} \) não pertence à coleção de conjuntos abertos de \( T \).

Portanto, na topologia \( T \), o conjunto \( \{b,c\} \) não é nem aberto nem fechado.

E assim por diante.