Topologia dos Conjuntos Abertos

Em outras palavras, a coleção T deve conter apenas subconjuntos de X que sejam classificados como “abertos” e ser estável em relação às operações de união e interseção.

Uma coleção de conjuntos é, portanto, um conjunto cujos elementos são outros conjuntos ou subconjuntos.

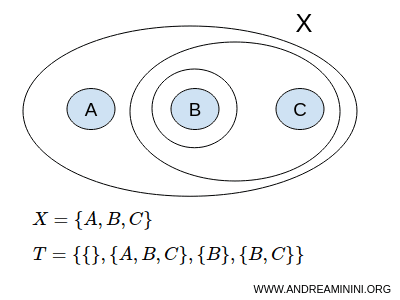
Nesse contexto, o conjunto X juntamente com a topologia T constituem um espaço topológico, normalmente indicado pelo par (X,T).

Observação. Para simplificar, muitas vezes se diz apenas que X é um espaço topológico. Convém, porém, lembrar que um espaço topológico é composto por dois elementos: a topologia T (coleção de subconjuntos) e o conjunto X.

Por que o conjunto vazio é sempre considerado aberto?

Em qualquer espaço topológico, o conjunto vazio é definido como aberto.

Essa convenção faz parte da própria estrutura da teoria e garante que os axiomas da topologia sejam internamente consistentes e completos.

Um Exemplo Prático

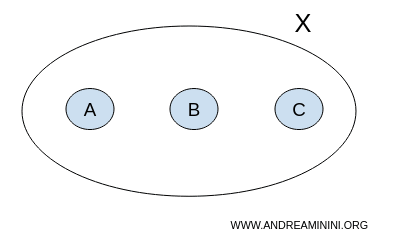
Considere o conjunto X formado por três elementos A, B e C:

$$ X = \{ A,B,C \} $$

Uma possível topologia T seria a coleção de subconjuntos { }, {A,B,C}, {B}, {B,C}:

$$ T = \{ \{ \},\{A,B,C \}, \{ B \}, \{ B,C \}  \} $$

Aqui, { } representa o conjunto vazio Ø, enquanto {A,B,C} corresponde ao próprio conjunto X, isto é, os subconjuntos impróprios de X.

Por definição, tanto o conjunto vazio quanto o conjunto completo X são conjuntos abertos.

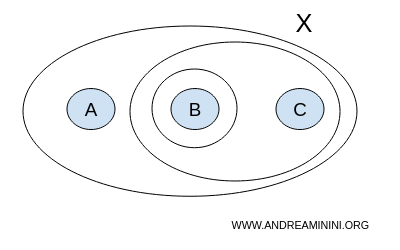
Uma topologia deve ser formada apenas por conjuntos abertos e, por definição, as operações de união e interseção entre eles produzem novos conjuntos abertos.

Neste caso, a união de subconjuntos de T permanece dentro da própria coleção T, o que significa que T é fechada em relação à união:

$$ \{ B \} \cup \{ B, C \} \subseteq \{ B, C \} \subseteq T$$

$$ \{ B \} \cup \{ A, B, C \} \subseteq \{ A, B, C \} \subseteq T$$

$$ \{ B \} \cup \{ \} \subseteq \{ B \} \subseteq T $$

$$ \{ B \} \cup \{ B \} \subseteq \{ B \} \subseteq T$$

De modo análogo, a interseção de subconjuntos de T também permanece na coleção T, o que garante que T é fechada em relação à interseção:

$$ \{ B \} \cap \{ B, C \} \subseteq \{ B \} \subseteq T$$

$$ \{ B \} \cap \{ A, B, C \} \subseteq \{ B \} \subseteq T$$

$$ \{ B \} \cap \{ \} \subseteq \{ \} \subseteq T $$

$$ \{ B \} \cap \{ B \} \subseteq \{ B \} \subseteq T$$

Portanto, a coleção T é de fato uma topologia sobre X, pois satisfaz todas as condições exigidas.

Exemplo 2

Agora, considere uma coleção ligeiramente diferente da anterior.

O conjunto X continua sendo o mesmo:

$$ X = \{ A,B,C \} $$

Neste caso, entretanto, a coleção T inclui também o subconjunto {A}, além de { }, {A,B,C}, {B} e {B,C}:

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

Essa nova coleção T não constitui uma topologia de X, pois não atende a todas as condições necessárias.

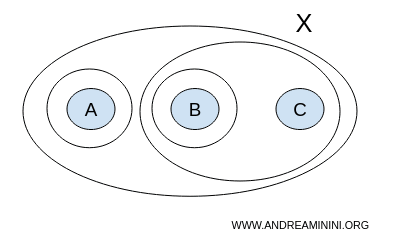
Por exemplo, a união dos subconjuntos {A} e {B} resulta em {A,B}, que não está contido em T:

$$\require{cancel} \{ A \} \cup \{ B \} = \{ A, B \} \cancel{\in} T  $$

Ou seja, {A} e {B} são considerados conjuntos abertos porque pertencem à coleção T, mas sua união não gera outro conjunto aberto, já que {A,B} não está incluído em T.

$$ T = \{ \{ \},\{A,B,C \}, \{ A \}, \{ B \}, \{ B,C \}  \} $$

Isso viola uma das condições fundamentais da definição de topologia.

Logo, a coleção T não pode ser considerada uma topologia de X.

E assim por diante.