Conjuntos Fechados

Um conjunto $ B $ em um espaço topológico $ X $ é dito fechado se, para cada elemento do complemento $ u \in X - B $, existir uma vizinhança inteiramente contida em $ X - B $.
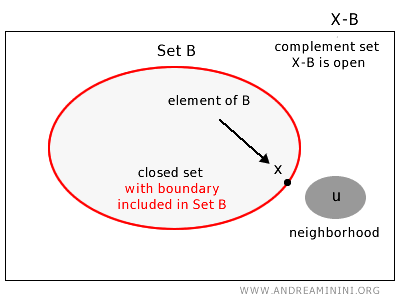
exemplo de um conjunto fechado

Em outras palavras, um conjunto é fechado quando contém todos os seus pontos de fronteira.

De forma mais rigorosa, um conjunto $ B $ em um espaço topológico $ X $ é fechado se o seu complemento $ X - B $ for aberto.

Observação: Isso implica que em $ B $ há pelo menos um ponto ao redor do qual não é possível encontrar uma vizinhança totalmente contida em $ B $.

Um exemplo prático
O complemento de um conjunto fechado
Exemplo
Propriedades dos Conjuntos Fechados
Exemplo
Notas Adicionais

Um exemplo prático

Consideremos a reta real $ \mathbb{R} $ e um intervalo fechado.

O que é um intervalo fechado? Um intervalo fechado em $ \mathbb{R} $ é o conjunto de todos os pontos $ x $ que satisfazem $ a \leq x \leq b $, onde $ a $ e $ b $ são números reais com $ a < b $, incluindo os extremos.

Os intervalos fechados são denotados por $[a,b]$, em que os colchetes indicam que os extremos $ a $ e $ b $ pertencem ao conjunto.

Por exemplo, o intervalo fechado $[3,10]$ é um conjunto fechado na reta real $ \mathbb{R} $.

Nesse caso, o conjunto $ B $ é formado por todos os números entre 3 e 10, incluindo os limites.

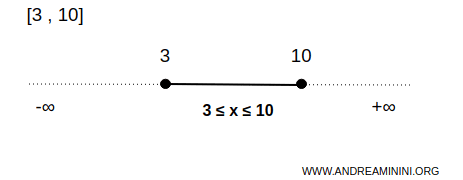
exemplo de um intervalo fechado

Isso significa que qualquer ponto $ x $ que satisfaça $ 3 \leq x \leq 10 $ pertence ao conjunto, incluindo os extremos $ x=3 $ e $ x=10 $.

No entanto, nem todos os pontos possuem uma vizinhança totalmente contida em $[3,10]$.

Por exemplo, qualquer vizinhança em torno do extremo $ x=3 $ incluirá inevitavelmente números menores que 3, que não fazem parte do intervalo.

Observação: Mesmo uma vizinhança infinitesimal, como $ 3 \pm 0.00000001 $, não estaria inteiramente dentro de $[3,10]$, pois $ 3 - 0.00000001 < 3 $. O mesmo raciocínio vale para o extremo superior $ x=10 $.

Esse é um exemplo elementar de conjunto fechado em uma dimensão.

Outros exemplos de conjuntos fechados

A mesma ideia se estende ao plano ($\mathbb{R}^2$).

Consideremos, por exemplo, o conjunto de pontos de um disco de raio $ r=1 $ e centro na origem $(0,0)$:

$$ x^2 + y^2 \leq 1 $$

Essa desigualdade descreve o conjunto de todos os pontos cuja distância ao centro $(0,0)$ é menor ou igual a 1, incluindo tanto os pontos internos quanto os da circunferência.

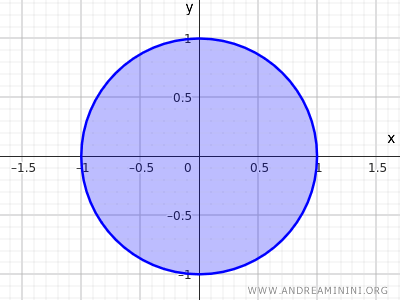
exemplo de um conjunto fechado no espaço bidimensional

Esse é mais um exemplo de conjunto fechado.

Observe que os pontos da circunferência $ x^2 + y^2 = 1 $ não possuem vizinhanças totalmente contidas dentro do disco fechado.

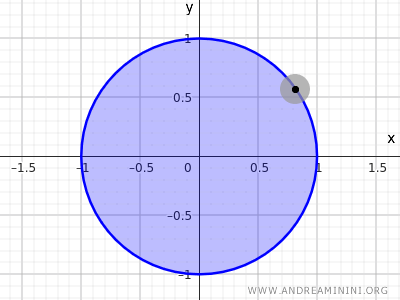
exemplo de um conjunto fechado

Observação: Em topologia, a circunferência definida por $ x^2 + y^2 = 1 $ não é nem aberta nem fechada em $ \mathbb{R}^2 $, pois contém apenas os pontos da borda e exclui o interior. Já o conjunto definido por $ x^2 + y^2 \leq 1 $, que abrange os pontos internos e os da circunferência, é um exemplo de conjunto fechado, pois inclui todos os pontos de fronteira.

Pelo mesmo princípio, o conceito de conjunto fechado se aplica ao espaço tridimensional (esfera sólida) e, de forma análoga, ao espaço $ n $-dimensional (uma $ n $-esfera fechada).

O complemento de um conjunto fechado

Em um espaço topológico $ X $, o complemento de um conjunto fechado $ C $ é um conjunto aberto, denotado por $ X - C $.

Ou seja, se $ C $ é fechado em $ X $, então o complemento $ X - C $ é necessariamente aberto.

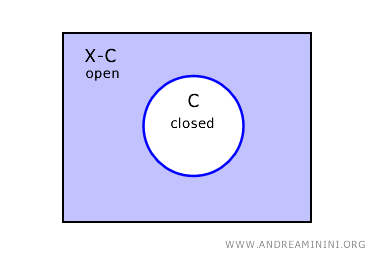
o complemento de um conjunto fechado

Reciprocamente, se um conjunto $ U $ é aberto, o seu complemento $ X - U $ é fechado em $ X $.

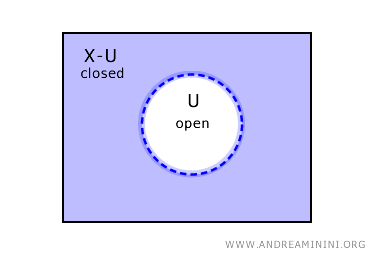
o complemento de um conjunto aberto

No entanto, essas não são as únicas possibilidades. Em certos espaços topológicos podem existir conjuntos que são ao mesmo tempo abertos e fechados, assim como conjuntos que não são nem abertos nem fechados.

Em outras palavras, um conjunto não ser fechado não implica que seja aberto, e não ser aberto não significa necessariamente que seja fechado.

Exemplo

Consideremos um espaço topológico $ (X, T) $, em que $ X = \{a,b,c,d\} $ possui quatro elementos e a topologia $ T $ é formada pelos seguintes abertos:

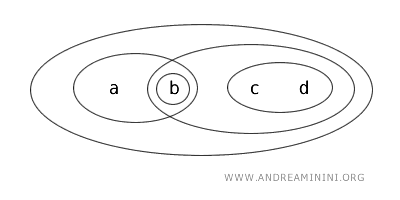
um exemplo prático

Os conjuntos abertos nessa topologia são: $ \{b\}, \{a,b\}, \{c,d\}, \{b,c,d\}, X $ e o conjunto vazio $ \varnothing $.

Analisemos alguns casos:

O conjunto $ \{b\} $ é aberto, pois está explicitamente incluído na definição da topologia.
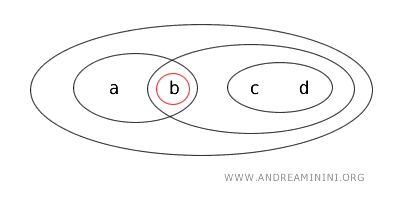
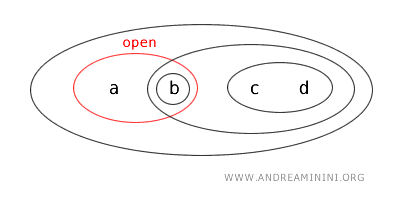
O conjunto $ \{a\} $ é fechado, porque seu complemento é aberto. De fato, $ X - \{a\} = \{b,c,d\} $ pertence à topologia.
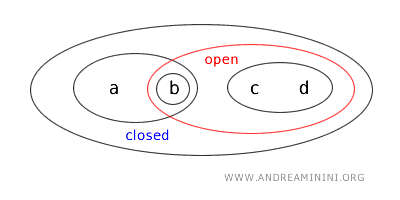
O conjunto $ \{a,b\} $ é simultaneamente aberto e fechado (clopen). Embora nas topologias usuais sobre $ \mathbb{R} $ isso seja raro, em espaços mais gerais um conjunto pode ser aberto e fechado ao mesmo tempo se o seu complemento também for aberto. Aqui, $ \{a,b\} $ é aberto pela definição da topologia e, como seu complemento $ X - \{a,b\} = \{c,d\} $ também é aberto, ele é igualmente fechado.
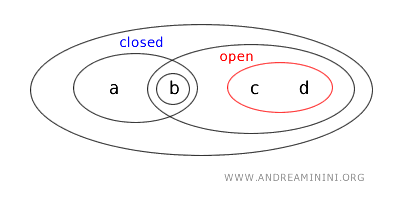
O conjunto $ \{b,c\} $ não é nem aberto nem fechado. Ele não aparece na lista de abertos da topologia, e o seu complemento $ X - \{b,c\} = \{a,d\} $ também não é aberto. Logo, não satisfaz nenhuma das duas condições.

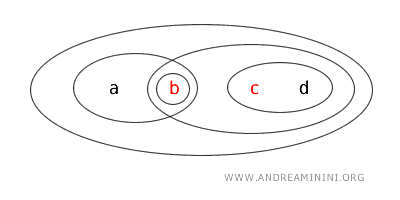
Esse exemplo mostra que, em um espaço topológico, um conjunto pode ser aberto, fechado, clopen (ambos) ou não se enquadrar em nenhum dos dois casos.

Propriedades dos Conjuntos Fechados

Um conjunto fechado é definido como o complemento de um conjunto aberto. Entre suas propriedades fundamentais destacam-se:

O conjunto vazio ($\varnothing$) e o espaço total $ X $ são sempre conjuntos fechados.
A interseção de qualquer coleção (finita ou infinita) de conjuntos fechados também é um conjunto fechado.
A união de um número finito de conjuntos fechados continua sendo um conjunto fechado.

Exemplo

Na topologia padrão do espaço euclidiano $ \mathbb{R}^n $, qualquer ponto isolado é um conjunto fechado.

Se tomarmos um ponto $ n $ na reta real ($ \mathbb{R}^1 $), o seu complemento é o conjunto de todos os pontos de $ \mathbb{R}^1 $ exceto $ n $.

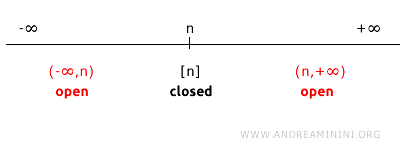
exemplo

O complemento de $\{n\}$ é a união de dois intervalos abertos: $(-\infty, n) \cup (n, +\infty)$.

Como $(-\infty, n)$ e $(n, +\infty)$ são abertos na topologia padrão, a sua união também é aberta.

Portanto, como o complemento de $\{n\}$ é aberto, concluímos que $\{n\}$ é um conjunto fechado.

No entanto, em algumas topologias os pontos individuais não são necessariamente conjuntos fechados. Isso depende diretamente da estrutura topológica adotada.

Consideremos, por exemplo, uma topologia sobre $ \mathbb{R} $ gerada pelos intervalos abertos $ (n, n+1) $, para cada inteiro $ n $. Nessa topologia, os pontos $ n $ não são conjuntos fechados, pois não podem ser descritos como o complemento de um aberto.
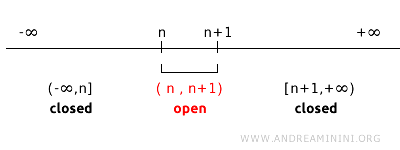
exemplo
Por exemplo, os conjuntos $ (1,2) $ e $ (2,3) $ são abertos nessa topologia. O complemento de $ (1,2) $ é $ (-\infty, 1] \cup [2, +\infty) $, enquanto o complemento de $ (2,3) $ é $ (-\infty, 2] \cup [3, +\infty) $.

Nesse contexto, não existe aberto cujo complemento seja exatamente $\{2\}$. De modo geral, para qualquer aberto da forma $ (n, n+1) $, o complemento é sempre uma união de intervalos fechados $ (-\infty, n] \cup [n+1, +\infty) $. Assim, nessa topologia, os pontos individuais não são conjuntos fechados, o que mostra como a noção de fechamento depende da topologia escolhida.

Notas Adicionais

Algumas observações importantes:

Conjuntos Fechados e Pontos de Acumulação
Um ponto de acumulação de um conjunto é aquele em cuja vizinhança, por menor que seja, sempre existe ao menos outro ponto do conjunto. Essa propriedade caracteriza os conjuntos fechados: um conjunto é fechado se contém todos os seus pontos de acumulação.

Exemplo: Consideremos o intervalo fechado $[0,1]$ na reta real. Esse conjunto contém todos os seus pontos de acumulação.

Por exemplo, o ponto $0.5$ em $[0,1]$ tem qualquer vizinhança aberta que contém infinitos pontos do intervalo, o que confirma que $0.5$ é ponto de acumulação.
exemplo de 0.5 como ponto de acumulação no intervalo fechado [0,1]

O mesmo ocorre nos extremos do intervalo. Por exemplo, $0$ é ponto de acumulação de $[0,1]$, pois qualquer vizinhança sua contém pontos do intervalo, como $0.1, 0.01, 0.001$ etc.
os extremos do intervalo fechado [0,1] são pontos de acumulação
Assim, todos os pontos de $[0,1]$ são pontos de acumulação do conjunto.

Um conjunto $ A $ é fechado se, e somente se, $ A = \overline{A} $
Em um espaço topológico, um conjunto $ A $ é fechado se coincide com o seu fecho, isto é, se $ A = \overline{A} $. O fecho de $ A $, denotado por $ \overline{A} $, é formado por todos os pontos de $ A $ juntamente com seus pontos de acumulação. Por definição, se $ A $ contém todos os seus pontos de acumulação, então ele é fechado.

E assim por diante.