Topologia Quociente

Sejam $X$ um espaço topológico e $A$ um conjunto que não é necessariamente um subconjunto de $X$. Suponha que exista uma aplicação sobrejetiva $p : X \rightarrow A$. Dizemos que um subconjunto $U \subseteq A$ é aberto se, e somente se, a sua pré-imagem $p^{-1}(U)$ for um aberto em $X$.

Em termos simples, um conjunto $U$ de $A$ é aberto na topologia quociente exatamente quando todos os pontos de $X$ que são enviados para $U$ pela aplicação $p$ formam um conjunto aberto em $X$.

ilustração da topologia quociente

Esse critério permite definir em $A$ uma nova topologia, chamada topologia quociente, construída a partir da topologia original de $X$ por meio da aplicação $p$.

Nessa situação, $A$ recebe o nome de espaço quociente, e a função $p$ é chamada de aplicação quociente.

O conjunto dos abertos de $A$ é frequentemente referido como a "topologia quociente induzida por $p$".

Em resumo, na topologia quociente, um conjunto é aberto sempre que a sua pré-imagem no espaço original for aberta.

É importante esclarecer um ponto que costuma causar confusão:

A pré-imagem de um aberto do espaço quociente $A$ é sempre um aberto de $X$, mas o inverso não é garantido.
A imagem direta de um aberto de $X$ não é, em geral, um aberto de $A$, pois a aplicação $p$ pode alterar a estrutura topológica do conjunto.

De forma geral, um espaço quociente é um espaço topológico obtido a partir de outro ao identificar, ou "colar", alguns de seus pontos segundo uma relação de equivalência.

Intuitivamente, trata-se de fundir certos pontos de um espaço seguindo uma regra precisa, para então estudar as propriedades topológicas do espaço resultante.

Por que a topologia quociente é importante? Porque ela permite estudar espaços muitas vezes mais complexos a partir de espaços mais simples, aproveitando o conhecimento já disponível sobre o espaço inicial $X$.

Explicação
Um exemplo concreto
Propriedades da topologia quociente

Explicação

A ideia de topologia quociente pode parecer abstrata à primeira vista, mas torna-se muito mais clara quando analisamos exemplos concretos.

A topologia quociente fornece um método formal para transformar uma figura geométrica colando entre si algumas de suas arestas ou faces.

Imagine, por exemplo, uma folha de papel quadrada. Ao colar dois lados opostos, obtemos um cilindro.

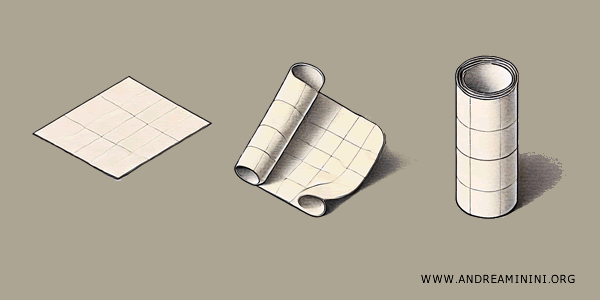
dobragem de uma folha para formar um cilindro

Se, em seguida, unirmos as bordas circulares do cilindro, obtemos uma superfície em forma de anel, chamada toro.

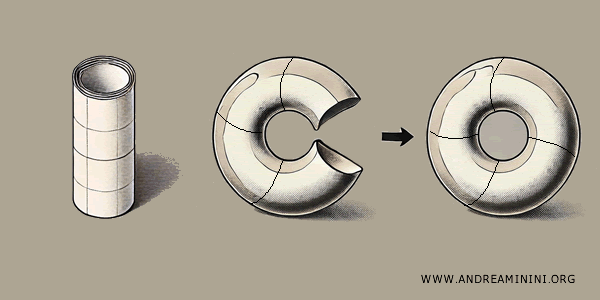
exemplo de um toro obtido a partir de um cilindro

Nesse processo, o quadrado é transformado primeiro em um cilindro e depois em um toro, simplesmente pela colagem adequada de suas bordas.

De modo análogo, a topologia quociente permite construir novos espaços topológicos a partir de espaços mais simples, identificando partes específicas desses espaços.

Essa abordagem é fundamental em matemática para o estudo das propriedades globais de superfícies e espaços topológicos.

Um exemplo concreto

Considere o espaço topológico $ X = [0, 1] $, munido da topologia usual, na qual os abertos são intervalos abertos ou uniões de intervalos abertos.

Nesse espaço:

Os conjuntos $X$ e $ \emptyset $ são abertos por definição.
Todo intervalo aberto $ (a,b) $, com $ 0 \leq a < b \leq 1 $, é um aberto de $X$.

Geometricamente, $X$ pode ser visto como um segmento de reta que liga os pontos $0$ e $1$.

representação gráfica do segmento [0,1]

Vamos agora construir um espaço quociente identificando as extremidades $0$ e $1$ do intervalo $[0,1]$, ou seja, tratando esses dois pontos como um único ponto.

Definimos a aplicação $ p : [0, 1] \rightarrow A $ da seguinte forma:

$$ p(x) = \begin{cases} p(0) & \text{se } x = 0 \text{ ou } x = 1 \\ \\ x & \text{se } 0 < x < 1 \end{cases} $$

O espaço quociente $A$ obtido dessa maneira pode ser visualizado como um círculo, no qual os pontos $0$ e $1$ foram identificados.

formação de um círculo por topologia quociente

Em termos intuitivos, curvamos o segmento e ligamos suas extremidades, obtendo uma figura fechada.

No novo espaço $A$, o ponto $P = \{0,1\}$ representa a imagem comum das duas extremidades pela aplicação $p$.

Para definir a topologia em $A$, precisamos decidir quais subconjuntos devem ser considerados abertos.

Por definição, um conjunto $U \subseteq A$ é aberto se a sua pré-imagem $p^{-1}(U)$ for um aberto de $[0,1]$.

Vejamos dois casos típicos:

Intervalo $ U = (a,b) $ que não contém $P$
A sua pré-imagem em $X$ é o intervalo aberto $ (a,b) $. Portanto, $U$ é aberto em $A$.
Intervalo $ U = (a,b) $ que contém $P = \{0,1\}$
A sua pré-imagem em $X$ é a união dos intervalos $ [0,a) \cup (b,1] $, ambos abertos em $X$. Assim, $U$ é um aberto de $A$.

Dessa forma, construímos um novo espaço topológico, o círculo, a partir do intervalo $[0,1]$.

Esse é um exemplo clássico de como a topologia quociente transforma um espaço simples em um espaço topologicamente mais rico.

Exemplo 2

No segundo exemplo, o objetivo é "enrolar" a reta real em torno de um círculo.

Considere a reta real $ \mathbb{R} $, que se estende infinitamente em ambas as direções.

A ideia é "dobrar" essa reta sobre um círculo, identificando cada número real com a sua parte fracionária.

Para isso, definimos a aplicação $ p(x) = x \mod 1 $.

De forma intuitiva, essa aplicação associa a cada número real apenas a sua parte decimal, isto é, o que vem depois da vírgula, posicionando-o no círculo.

Por exemplo, se $ x = 1{,}3 $, a sua parte decimal é 0,3, e esse ponto é colocado na posição correspondente a 0,3 no círculo. Se $ x = 2{,}7 $, a parte decimal é 0,7, que corresponde exatamente ao mesmo ponto que $0{,}7$.
enrolamento da reta real sobre um círculo

Observe que, sempre que $x$ aumenta de uma unidade, a sua imagem no círculo permanece a mesma.

Esse procedimento equivale a identificar os pontos 0 e 1, bem como todos os números que diferem entre si por um inteiro.

Analisemos agora alguns intervalos específicos.

Intervalo (0,1) em $ \mathbb{R} $
O intervalo $ (0,1) $ transforma-se em um arco aberto do círculo, sem incluir o ponto 0. Ele permanece aberto no espaço quociente, pois a sua pré-imagem em $ \mathbb{R} $ também é aberta.
Intervalo (1,2) em $ \mathbb{R} $
O intervalo $ (1,2) $ projeta-se exatamente sobre o mesmo arco que $ (0,1) $, já que $1 \mod 1 = 0$ e $2 \mod 1 = 0$. Portanto, não acrescenta nenhuma informação nova à topologia quociente.
Intervalo (0,2) em $ \mathbb{R} $
O intervalo $ (0,2) $ cobre toda a circunferência, passando duas vezes por cada ponto. Embora seja aberto em $ \mathbb{R} $, a sua imagem no círculo coincide com o conjunto inteiro, que neste caso é simultaneamente aberto e fechado (clopen), pois o círculo não possui bordo.

Observação: Este exemplo mostra que a imagem de um aberto de $ \mathbb{R} $ não é, em geral, um aberto no espaço quociente.

Por outro lado, todo aberto do círculo possui sempre uma pré-imagem aberta em $ \mathbb{R} $.

De fato, "desenrolar" um aberto do círculo em $ \mathbb{R} $ resulta em uma união infinita de intervalos abertos.

No entanto, o recíproco não vale em geral: um aberto de $ \mathbb{R} $ não precisa ter uma imagem aberta no círculo.

Conclusão

Assim, não se pode assumir que um aberto da reta real se projete automaticamente em um aberto do círculo, pois a aplicação de projeção pode alterar de maneira significativa a estrutura topológica do conjunto.

Exemplo 3

Neste terceiro exemplo, mostramos como construir uma topologia quociente a partir de uma sequência finita de inteiros consecutivos, identificando o primeiro ($m$) e o último ($n$) elementos da sequência $ \{ m, m+1, \ldots, n \} \subset \mathbb{Z} $.

Consideremos, em particular, a sequência dos sete inteiros consecutivos de 1 a 7:

$$ I_7 = \{1, 2, 3, 4, 5, 6, 7\} $$

Esse conjunto é um intervalo discreto, pois é formado por inteiros sucessivos no conjunto dos números inteiros.

Identificamos agora o primeiro elemento (1) com o último (7). Intuitivamente, é como se fechássemos uma linha discreta, transformando-a em uma estrutura cíclica semelhante a um círculo.

criação de um círculo numérico a partir de um intervalo discreto

O resultado é uma estrutura conhecida como ciclo discreto ou círculo numérico $ C_6 $, composta por 6 pontos dispostos em forma de anel.

Nesse ciclo, cada ponto é adjacente exatamente a dois vizinhos, segundo a relação de adjacência adotada.

Temos, portanto, um exemplo legítimo de topologia quociente, já que um novo espaço topológico é obtido a partir da identificação de pontos do espaço inicial.

Observação: Esse procedimento é análogo ao que ocorre quando identificamos as extremidades de um intervalo real $(a,b)$. A diferença é que, neste caso, trabalhamos com um conjunto finito e discreto, o que leva a propriedades topológicas distintas.

O círculo numérico também aparece no contexto da topologia digital (ou topologia numérica), na qual os pontos são relacionados por noções de adjacência discreta.

Trata-se de um espaço discreto, no qual se estudam conceitos como conexidade digital e abertos digitais.

Observação: Em topologia digital, um conjunto $ U $ é considerado aberto se, para todo ponto $ x \in U $, todos os seus vizinhos imediatos, de acordo com a noção de adjacência escolhida, também pertencem a $ U $. São exemplos usuais a adjacência-2 em 1D, adjacência-4 ou -8 em 2D e adjacência-6 ou -18 em 3D.

É importante destacar que a topologia quociente e a topologia digital pertencem a quadros conceituais diferentes.

Em outras palavras, embora o círculo numérico possa ser obtido por identificação de pontos, ele se insere em uma categoria distinta no âmbito da topologia discreta.

Exemplo 4

Consideremos agora o conjunto dos números reais $ \mathbb{R} $, munido da sua topologia usual, e definamos uma aplicação quociente $ p : \mathbb{R} \to \{a, b, c\} $ da seguinte forma:

$$ p(x) = \begin{cases} a \quad \text{se} \quad x < 0 \\ \\ b \quad \text{se} \quad x = 0 \\ \\ c \quad \text{se} \quad x > 0 \\ \end{cases} $$

Essa aplicação pode ser interpretada como uma contração do conjunto dos reais estritamente negativos em um único ponto $ a $, o envio do ponto $ 0 $ para $ b $ e a identificação de todos os reais estritamente positivos em um único ponto $ c $.

A topologia quociente induzida por $ p $ é completamente determinada pelas pré-imagens desses três pontos.

De fato, temos:

$ p^{-1}(a) = (-\infty, 0) $, que é um aberto de $ \mathbb{R} $,
$ p^{-1}(b) = \{0\} $, que não é um aberto em $ \mathbb{R} $,
$ p^{-1}(c) = (0, \infty) $, que também é um aberto de $ \mathbb{R} $.

Em uma topologia quociente, um subconjunto de $ \{a, b, c\} $ é aberto se, e somente se, a sua pré-imagem por $ p $ for um aberto de $ \mathbb{R} $. Como consequência, são abertos nessa topologia:

O singleton $ \{a\} $,
O singleton $ \{c\} $,
A união $ \{a, c\} $, cuja pré-imagem é $ \mathbb{R} \setminus \{0\} $.

Além disso, os conjuntos $ \emptyset $ e $ \{a, b, c\} $ são sempre abertos em qualquer topologia, inclusive na topologia quociente:

$ \{a, b, c\} $ é aberto porque a sua pré-imagem é $ \mathbb{R} $, aberto na topologia usual,
$ \emptyset $ é aberto porque a sua pré-imagem é o próprio conjunto vazio.

Por outro lado, o singleton $ \{b\} $ não é aberto na topologia quociente, pois a sua pré-imagem $ \{0\} $ não é um aberto de $ \mathbb{R} $.

Concluímos, portanto, que os únicos abertos da topologia quociente sobre $ \{a, b, c\} $ são $ \emptyset $, $ \{a\} $, $ \{c\} $, $ \{a, c\} $ e $ \{a, b, c\} $. O ponto $ b $, correspondente ao número 0, não pertence a nenhum aberto próprio não trivial, pois não admite nenhuma vizinhança aberta no espaço de origem.

Do ponto de vista topológico, o ponto $ b $ comporta-se como uma singularidade topológica, isto é, um ponto que rompe a estrutura local herdada do espaço original.

Propriedades da topologia quociente

Apresentamos a seguir algumas propriedades fundamentais válidas para toda topologia quociente:

Os conjuntos vazio e total são sempre abertos
Em qualquer topologia quociente, $ \emptyset $ e o conjunto total $ A $ são, por definição, abertos.
- Pré-imagem do conjunto vazio
  $ p^{-1}(\emptyset) = \emptyset $ é aberto em qualquer espaço topológico, logo $ \emptyset $ é aberto em $ A $.
- Pré-imagem do conjunto total
  $ p^{-1}(A) = X $, que é aberto em $ X $ por ser o conjunto total.
Observação: Isso confirma que os conjuntos triviais, vazio e total, mantêm sempre o seu estatuto de abertos, inclusive nas topologias induzidas.
Uniões arbitrárias de abertos
Se cada $ U_i $ é aberto em $ A $, então a sua união também é um aberto:
$$ \left( \forall i,\ U_i \text{ aberto em } A \right) \Rightarrow p^{-1}\left( \bigcup U_i \right) = \bigcup p^{-1}(U_i) \text{ é aberto em } X. $$
Observação: Como a união de qualquer família de abertos é aberta em $ X $, essa propriedade é automaticamente herdada pela topologia quociente.
Interseções finitas de abertos
Se os conjuntos $ U_i $ são abertos em $ A $, então a sua interseção finita também é um aberto de $ A $, pois
$$ p^{-1}\left( \bigcap U_i \right) = \bigcap p^{-1}(U_i) \text{ é aberto em } X. $$
Observação: A estabilidade dos abertos por interseção finita em $ X $ garante que essa propriedade se reflita fielmente na topologia quociente.

Essas propriedades formam a base conceitual necessária para compreender a estrutura e o comportamento dos espaços topológicos quocientes.