Transformações Topológicas

Transformações topológicas são operações aplicadas a espaços topológicos que preservam propriedades essenciais, como conectividade e continuidade.

Essas transformações desempenham um papel fundamental no estudo da topologia, um ramo da matemática que investiga as propriedades dos espaços que permanecem invariantes sob transformações contínuas.

Entre as principais características das transformações topológicas, destacam-se:

• Continuidade
  Uma transformação topológica deve ser contínua, isto é, pequenas variações na entrada resultam em pequenas variações na saída.
• Conectividade e proximidade
  Essas transformações preservam as noções de vizinhança e conexão. Se dois pontos estão próximos ou conectados no espaço original, permanecerão assim no espaço transformado.
• Deformação sem rasgar ou colar
  Os objetos podem ser esticados, comprimidos ou dobrados, mas não podem ser rasgados nem colados. Um exemplo clássico é a equivalência entre uma rosquinha e uma xícara de café: ambos têm um único "furo" e, portanto, são topologicamente equivalentes.

Aplicações: As transformações topológicas são utilizadas em diversas áreas, da matemática pura - como na teoria dos nós e na topologia algébrica - até no estudo de propriedades de objetos que permanecem invariantes sob deformações contínuas.

Tipos de Transformações Topológicas

Na topologia, as transformações são geralmente classificadas de acordo com a preservação de determinadas propriedades topológicas.

A seguir, alguns tipos fundamentais de transformações:

• Homeomorfismos
  Um homeomorfismo é uma transformação contínua com inversa contínua. Em termos simples, permite converter um espaço em outro e reverter o processo sem "quebrar" nem "colar". Esse conceito é central na topologia. Um exemplo famoso é a equivalência entre a xícara e a rosquinha.
• Isotopias
  A isotopia é um caso particular de homeomorfismo, em que cada estágio da transformação também é um homeomorfismo. Imagine deslizar um nó ao longo de um fio sem apertá-lo nem afrouxá-lo: cada fase desse movimento corresponde a uma isotopia.
• Homotopias
  As homotopias mostram como uma função pode ser "deformada" em outra, preservando certas propriedades topológicas. São menos restritivas do que os homeomorfismos. Um exemplo é esticar uma mola e depois deixá-la voltar: as formas intermediárias durante esse processo são homotópicas.
• Difeomorfismos
  Um difeomorfismo é um homeomorfismo que, além disso, é diferenciável. É especialmente relevante na topologia diferencial, onde suavidade e diferenciabilidade das superfícies são cruciais. Por exemplo, transformar uma esfera flexível em um elipsoide alongado.

Esses diferentes tipos de transformações ressaltam aspectos distintos da continuidade e da deformabilidade dos espaços e funções em topologia.

O uso de cada uma delas depende do contexto específico: topologia geral, topologia algébrica ou topologia diferencial.

A Diferença Entre Transformações Geométricas e Topológicas

As transformações geométricas e topológicas se diferenciam tanto em suas propriedades quanto em suas aplicações:

• Transformações Geométricas
  Alteram objetos no espaço preservando propriedades geométricas como distâncias, ângulos e formas. Exemplos: translações, rotações, reflexões e ampliações/reduções.

  Por exemplo, uma rotação preserva distâncias e ângulos, mas muda a orientação.

• Transformações Topológicas
  Alteram os espaços preservando propriedades topológicas, como conectividade e continuidade, mas não necessariamente distâncias ou ângulos. São transformações muito mais flexíveis, que permitem esticar e deformar figuras sem cortar nem colar.

  Por exemplo, em topologia, uma rosquinha pode ser transformada em uma xícara de café porque ambas possuem um único furo.

Enquanto as transformações geométricas se concentram em movimentos ou alterações de forma preservando medidas e proporções, as transformações topológicas enfatizam deformações que preservam conectividade e continuidade, sem se preocupar com a forma ou o tamanho exato.

Uma transformação pode ser ao mesmo tempo geométrica e topológica?

Sim. Algumas transformações não apenas preservam propriedades geométricas, como ângulos, comprimentos e formas, mas também são contínuas e mantêm propriedades topológicas, como conectividade e continuidade.

Veja alguns exemplos práticos:

• Isometrias
  Isometrias, como translações, rotações e reflexões, preservam distâncias entre pontos e ângulos. Por isso, são simultaneamente transformações geométricas e topológicas. Do ponto de vista da topologia, são homeomorfismos, pois também possuem inversa contínua.
  
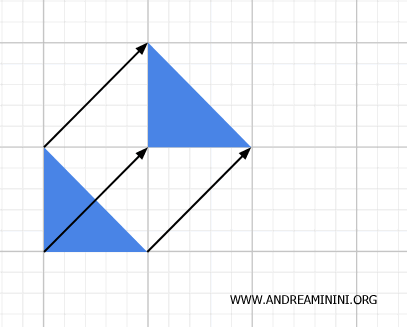
• Similaridades
  Similaridades modificam o tamanho dos objetos, mas preservam a forma. Incluem ampliações e reduções que mantêm ângulos e proporções relativas. São consideradas transformações geométricas por afetarem forma e tamanho, mas também topológicas por preservarem continuidade e conectividade.

Esses exemplos mostram que propriedades geométricas e topológicas não são, necessariamente, excludentes. Em alguns casos, uma transformação pode ser ao mesmo tempo geometricamente relevante e topologicamente válida.

E assim por diante.