Espaço de Hausdorff

Um espaço de Hausdorff é um tipo de espaço topológico no qual quaisquer dois pontos distintos podem ser separados por vizinhanças abertas que não se intersectam. Essa propriedade garante que cada ponto possa ser identificado de forma precisa e inequívoca dentro do espaço.

De maneira intuitiva, em um espaço de Hausdorff é sempre possível encontrar vizinhanças abertas $ U $ e $ V $ para quaisquer dois pontos $ x $ e $ y $, de modo que essas vizinhanças não tenham pontos em comum, isto é, $ U \cap V = \emptyset $.

Essa condição fornece uma noção rigorosa de separabilidade, alinhada à nossa intuição geométrica sobre distância e proximidade no espaço euclidiano.

Os espaços de Hausdorff são fundamentais em análise e geometria porque simplificam o estudo da convergência de sequências e diversas outras construções essenciais da topologia.

Um resultado importante é que, em qualquer espaço de Hausdorff, os conjuntos formados por um único ponto são conjuntos fechados.

De fato, o complemento de um ponto isolado, ou seja, o conjunto formado por todos os outros pontos do espaço, é sempre um conjunto aberto.

Exemplos práticos
Observações

Exemplos práticos

Exemplo 1

Considere a topologia padrão, usada para descrever a estrutura topológica da reta real $\mathbb{R}$.

exemplo da reta real

Nessa topologia, conjuntos formados por um único ponto não são abertos.

Explicação: Na topologia padrão, um conjunto aberto deve conter, junto de cada um de seus pontos, um intervalo aberto inteiro ao seu redor. Como entre quaisquer dois números reais há infinitos outros valores, um conjunto reduzido a um único elemento $ \{x\} $ não pode satisfazer essa exigência. Falta-lhe a "folga" necessária para incluir todos os pontos vizinhos exigidos por uma vizinhança aberta. Por isso, pontos isolados não podem ser conjuntos abertos na topologia usual de $\mathbb{R}$.

Por outro lado, o complemento de um ponto $ \mathbb{R} \setminus \{x\} $ é sempre um conjunto aberto.

a vizinhança do ponto individual é um conjunto aberto

Isso mostra que qualquer ponto $ \{x\} $ é um conjunto fechado, pois seu complemento é aberto.

Além disso, a topologia padrão de $\mathbb{R}$ define um espaço de Hausdorff, porque para quaisquer dois pontos distintos $ a $ e $ b $ é possível construir vizinhanças abertas que os separem completamente.

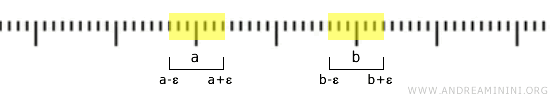
vizinhanças dos pontos a e b

Por exemplo, se $ a < b $, podemos considerar os intervalos abertos $ (a-\epsilon, a+\epsilon) $ e $ (b-\epsilon, b+\epsilon) $, escolhendo $ \epsilon $ suficientemente pequeno para garantir que $ a+\epsilon < b-\epsilon $. Assim, asseguramos que as vizinhanças construídas sejam disjuntas.

Em resumo, o fato de pontos individuais serem conjuntos fechados na topologia padrão confirma que $\mathbb{R}$, com sua topologia usual, é um espaço de Hausdorff.

Exemplo 2

Considere um espaço topológico definido sobre o conjunto $ X = \{1,2,3\} $, equipado com a topologia discreta.

Na topologia discreta, cada ponto de $ X $ é, por definição, um conjunto aberto.

Isso significa que todos os subconjuntos de $ X $ são abertos:

o conjunto vazio $ \emptyset $
os conjuntos unitários $ \{1\} $, $ \{2\} $, $ \{3\} $
os subconjuntos com dois elementos $ \{1, 2\} $, $ \{1, 3\} $, $ \{2, 3\} $, obtidos como uniões ou interseções de abertos
o conjunto total $ \{1, 2, 3\} $

No total, existem $ 2^3 = 8 $ conjuntos abertos, ou seja, todos os subconjuntos possíveis de $ X $.

Nessa topologia, o espaço é sempre um espaço de Hausdorff.

Por definição, um espaço é de Hausdorff quando, para quaisquer pontos distintos $ x $ e $ y $, existem vizinhanças abertas $ U $ e $ V $ tais que $ U \cap V = \emptyset $, com $ x \in U $ e $ y \in V $.

Na topologia discreta, como cada ponto é um aberto, para quaisquer $ x \neq y $ em $ X = \{1,2,3\} $, basta escolher $ U = \{x\} $ e $ V = \{y\} $.

Como $ U \cap V = \emptyset $, a condição de Hausdorff é automaticamente satisfeita.

Por exemplo, escolhendo $ x = \{1\} $ e $ y = \{2\} $, com $ U = \{1\} $ e $ V = \{2\} $, obtemos:

$$ \{1\} \cap \{2\} = \emptyset $$

Isso confirma que, na topologia discreta, quaisquer dois pontos podem ser separados por vizinhanças abertas.

O mesmo vale para qualquer outro par de elementos de $ X $.

Na topologia discreta, pontos individuais são abertos ou fechados?

Essa dúvida é comum no início. Se a topologia discreta é um espaço de Hausdorff, então os conjuntos unitários $ \{x\} $ deveriam ser fechados. Mas, pela definição dessa topologia, eles também são abertos. Como resolver essa aparente contradição?

A resposta é direta: em topologia, um conjunto pode ser simultaneamente aberto e fechado. Conjuntos com essa característica recebem o nome de conjuntos clopen. Nessa linguagem, "fechado" não significa necessariamente o oposto de "aberto".

Na topologia discreta, todo conjunto unitário $ \{x\} $ é fechado porque o seu complemento, formado pelos pontos restantes do espaço, é aberto. Como todos os subconjuntos são abertos, seus complementos também são abertos, e portanto os unitários são fechados.

Por exemplo, se $ X = \{1,2,3\} $ e observamos o ponto $ \{1\} $, ele é aberto pela definição da topologia discreta. Ao mesmo tempo, é fechado porque seu complemento, $ X \setminus \{1\} = \{2,3\} $, também é aberto. Em topologia, o complemento de um aberto é sempre fechado.

Concluindo, os pontos individuais $ \{x\} $ na topologia discreta são ao mesmo tempo abertos e fechados, pois todos os subconjuntos são abertos e seus complementos também.

Aberto
Cada ponto é aberto por definição na topologia discreta.
Fechado
O complemento $ X \setminus \{x\} $, contendo todos os demais elementos, é aberto. Logo, $ \{x\} $ é fechado.

Em resumo, os pontos individuais $ \{x\} $ são abertos porque todos os subconjuntos são abertos, e são fechados porque seus complementos também são abertos.

Uma diferença essencial entre a topologia discreta e a topologia padrão é que, na topologia padrão, nem todo subconjunto é aberto. Apenas os conjuntos que satisfazem a definição de vizinhança aberta para cada um de seus pontos são considerados abertos.

Observações

Algumas propriedades e consequências fundamentais dos espaços de Hausdorff:

Em um espaço de Hausdorff, toda sucessão convergente possui um único limite
Em um espaço de Hausdorff $ X $, qualquer sucessão convergente converge para um único ponto $ x \in X $. Se uma mesma sucessão pudesse convergir para dois pontos distintos, haveria vizinhanças abertas sobrepostas, o que contradiz a definição de espaço de Hausdorff.

Demonstração: Seja $ X $ um espaço de Hausdorff (por exemplo, a reta real $ X = \mathbb{R} $). Suponha, por absurdo, que exista uma sucessão $ x_1, x_2, x_3, \dots $ que converge para dois pontos distintos $ x $ e $ y $ em $ X $. Pela definição de convergência em um espaço topológico, existe um inteiro $ N $ tal que, para todo $ n > N $, os termos $ x_n $ pertencem a um entorno $ A $ de $ x $.

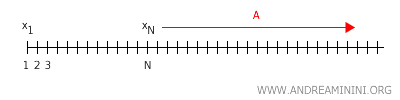
uma sucessão convergindo para x

Da mesma forma, existe um inteiro $ M $ tal que, para todo $ n > M $, os pontos $ x_n $ pertencem a um entorno $ B $ de $ y $.

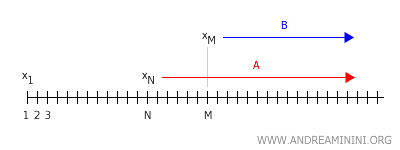
a sucessão também convergindo para y

Se $ M > N $, então alguns elementos de $ A $ também pertenceriam a $ B $, o que implica $ A \cap B \neq \emptyset $, contradizendo a propriedade de separação de Hausdorff. Logo, em um espaço de Hausdorff, uma sucessão não pode convergir para mais de um ponto.