Conjuntos Abertos

Um conjunto A é chamado aberto se, para todo elemento x pertencente a A (x∈A), existe uma vizinhança que ainda está contida no próprio conjunto.

 

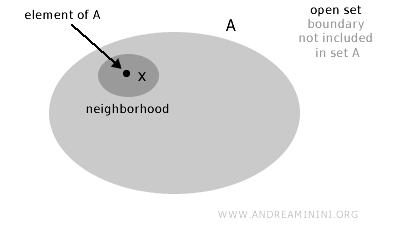
Em outras palavras, um conjunto é aberto quando, de forma intuitiva, suas "fronteiras" não fazem parte dele.

De maneira mais formal, um conjunto A em um espaço topológico X é aberto se, para cada ponto x em A, existe uma vizinhança de x totalmente contida em A.

Observação. Isso significa que, em torno de qualquer ponto do conjunto, sempre é possível encontrar uma "região" que permanece inteiramente dentro dele, sem "encostar" na borda externa.

Um Exemplo Prático

Um exemplo simples de conjunto aberto em uma reta é um intervalo aberto.

O que é um intervalo aberto? Um intervalo aberto de R é o conjunto dos números reais x tais que a < x < b, onde a e b são dois números reais que satisfazem a < b.

Esse intervalo é denotado por (a,b), onde os parênteses arredondados indicam que os extremos a e b não pertencem ao conjunto.

Por exemplo, o intervalo aberto (3,10) é um conjunto aberto na reta real.

Nesse caso, o conjunto A contém infinitos números entre 3 e 10, excluindo os extremos.

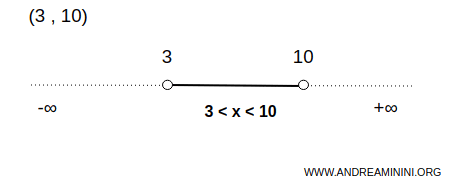
Isso quer dizer que, para qualquer ponto x dentro desse intervalo, existe sempre um pequeno intervalo aberto em torno de x que está completamente contido em (3,10).

Por exemplo, para o ponto x=3.1, posso tomar o intervalo aberto (3.09,3.11), que fica inteiramente dentro de (3,10).

O mesmo vale para qualquer outro ponto do intervalo (3,10), pois entre dois números reais sempre existem infinitos números reais.

Observação. Mesmo que eu escolha um número real muito próximo da borda do intervalo (3,10), como 3.001, ainda consigo construir uma vizinhança 3.001±0.00000001 que contém infinitos números reais dentro do intervalo aberto (3,10).

Esse é um exemplo simples, unidimensional, de conjunto aberto.

Outros Exemplos

O mesmo raciocínio pode ser estendido ao espaço bidimensional, como o plano.

Por exemplo, o conjunto de pontos de um círculo com raio r=1 e centro na origem (0;0).

$$ x^2+y^2<1 $$

Essa desigualdade descreve o conjunto de todos os pontos cuja distância até o centro (0,0) é menor que 1, ou seja, não inclui os pontos da circunferência, apenas os que estão dentro do círculo.

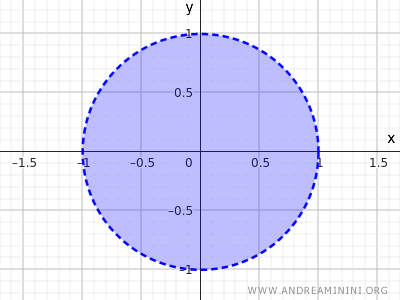
Mais um exemplo de conjunto aberto.

E quando um conjunto é fechado?

Para que seja fechado, basta incluir também os pontos da circunferência.

$$ x^2+y^2 \le 1 $$

Nesse caso, já não vale a condição de que todo elemento do conjunto possua uma vizinhança totalmente contida nele.

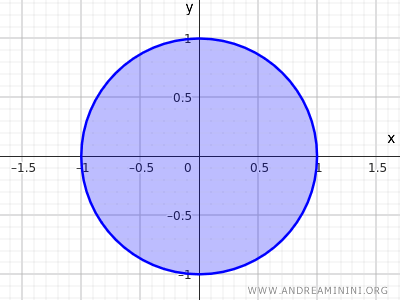
No conjunto fechado, os pontos da circunferência não têm vizinhanças inteiramente contidas dentro do conjunto.

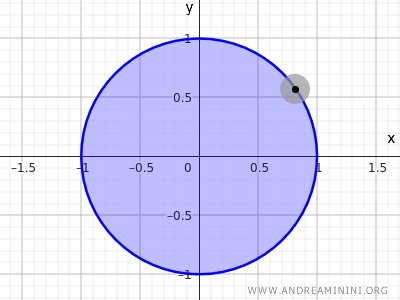
Observação. Em topologia, a equação do círculo $ x^2+y^2=1 $ não define um conjunto aberto nem fechado em R², pois considera apenas os pontos da circunferência, sem os internos. Já o conjunto definido pela desigualdade $ x^2+y^2<1 $, que inclui os pontos internos mas não os da borda, é um exemplo de conjunto aberto. Se acrescentarmos também os pontos da circunferência $ x^2+y^2\le 1 $, teremos um conjunto fechado.

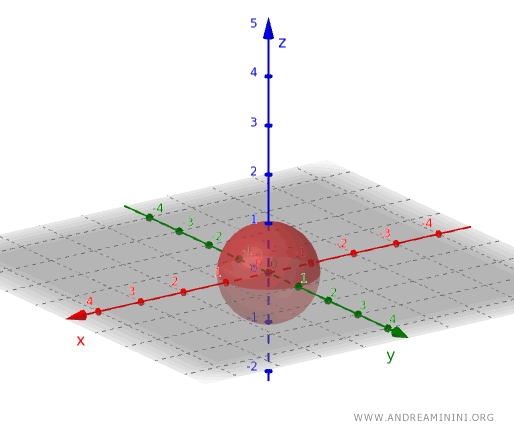
Pelo mesmo princípio, um conjunto aberto em três dimensões pode ser construído considerando, por exemplo, todos os pontos dentro de uma esfera, mas sem os da sua superfície.

Escolhendo uma Topologia

Intervalos abertos são muito úteis porque são intuitivos e dão uma noção imediata do que significa um conjunto aberto.

No entanto, o conceito é bem mais abstrato e não deve ser reduzido apenas a intervalos abertos.

Por isso, depois de entender a ideia básica, vale a pena explorá-la com mais profundidade.

O conceito de conjunto "aberto" depende da topologia escolhida para o espaço.

A ideia central é que a definição de conjunto aberto pode variar radicalmente conforme a topologia adotada para o espaço.

Em certos espaços, um conjunto que parece "fechado" na topologia usual pode ser considerado "aberto" em outra.

Em outras palavras, qualquer conjunto pode ser aberto, dependendo da topologia definida para o espaço.

O que é uma topologia? Uma topologia em um espaço é, essencialmente, uma coleção de conjuntos considerados "abertos" de acordo com certas regras: por exemplo, a união arbitrária de conjuntos abertos ainda é aberta, e a interseção de um número finito de conjuntos abertos também resulta em um conjunto aberto.

Por isso, não é recomendável limitar a noção apenas aos exemplos mais comuns e intuitivos de conjuntos abertos, como intervalos ou discos abertos.

Na topologia, a definição de "conjunto aberto" é muito mais ampla e pode englobar conjuntos que, à primeira vista, não pareceriam ser.

Um Exemplo Prático

Considere o espaço \( \{a, b\} \), formado por apenas dois elementos.

Nesse espaço, é possível definir pelo menos duas topologias distintas: a topologia trivial e a topologia discreta.

• Topologia Trivial
  Na topologia trivial em \( \{a, b\} \), os únicos conjuntos abertos são o conjunto vazio \( \emptyset \) e o próprio espaço \( \{a, b\} \). É a topologia mais simples possível, praticamente sem nenhuma "estrutura aberta" além do conjunto total e do vazio.
• Topologia Discreta
  Na topologia discreta, todo subconjunto de \( \{a, b\} \) é aberto. Isso significa que \( \{a\} \), \( \{b\} \), \( \{a, b\} \) e \( \emptyset \) são todos abertos. A topologia discreta é a mais "rica" em termos de conjuntos abertos, já que qualquer combinação de pontos forma um conjunto aberto.

Agora, analisemos o conjunto \( \{a\} \) em ambas as topologias:

• Na topologia trivial, o conjunto {a} não é aberto
  Os únicos conjuntos abertos não-vazios são \( \{a, b\} \) e o próprio espaço, além do vazio.
• Na topologia discreta, o conjunto {a} é aberto
  Nessa topologia, todo subconjunto de \( \{a, b\} \), incluindo \( \{a\} \) e \( \{b\} \), é aberto por definição.

Portanto, o conjunto \( \{a\} \) é aberto na topologia discreta, mas não na trivial.

Esse exemplo simples mostra como a definição de conjunto aberto está diretamente vinculada à topologia adotada.

Teorema do Conjunto Aberto

Teorema 1

Sejam um conjunto aberto X e uma topologia T que, juntos, formam um espaço topológico (X,T). Um subconjunto S⊂X é aberto em (X,T) se, para todo elemento (ou ponto) s∈S, existir uma vizinhança U inteiramente contida em S, ou seja, U⊂S.

Pela própria definição, S é um conjunto aberto, pois faz parte do espaço topológico (X,T).

Assim, o subconjunto S pode ser entendido como a vizinhança de cada um de seus elementos (pontos) s∈S.

Daí resulta que a vizinhança U_s de qualquer elemento s∈S é, por sua vez, um conjunto aberto contido em S.

$$ x \in U_s ⊂ S ⊂ X $$

Um conjunto aberto pode ser visto como a união das vizinhanças abertas de seus pontos.

Portanto, se cada elemento (ponto) s∈S de um subconjunto S possui uma vizinhança U_s⊂S inteiramente contida em S, então S é aberto, já que é a união de conjuntos abertos.

Em outras palavras, um conjunto é aberto se, e somente se, para todo ponto em seu interior existir uma vizinhança desse ponto totalmente contida no conjunto.

Exemplo. Imagine uma mesa coberta de bolinhas de gude. Cada bolinha representa um ponto de certo conjunto. Dizer que esse conjunto é "aberto" significa que existe espaço suficiente em volta de cada bolinha para movimentá-la sem ultrapassar a borda da mesa. Se, para toda bolinha, é possível traçar um círculo ao seu redor que permaneça inteiramente dentro da mesa (sem tocar as bordas), então o conjunto de bolinhas representa um "conjunto aberto". Em essência, a abertura do conjunto indica que, não importa qual bolinha eu escolha, sempre haverá uma região em volta dela que ainda pertence ao conjunto de bolinhas da mesa.

Teorema 2

Seja \( X \) um conjunto e \( B \) uma base para uma topologia em \( X \). Um subconjunto \( A \subset X \) é aberto na topologia gerada por \( B \) se, e somente se, para cada elemento \( x \in A \), existir um elemento da base \( B_x \in B \) tal que \( x \in B_x \) e \( B_x \subseteq A \).

Esse teorema evidencia uma característica fundamental das topologias construídas a partir de uma base.

De maneira simples, cada ponto de um conjunto aberto \( A \) deve estar contido em uma "vizinhança" \( B_x \), pertencente à base, que esteja inteiramente dentro de \( A \).

Isso confirma que o conjunto \( A \) é de fato aberto na topologia gerada por \( B \).

Demonstração. Se A é aberto na topologia gerada pela base B em X, com A ⊂ X, então, por definição, A é a união de elementos da base. Logo, cada ponto x de A pertence a pelo menos um elemento da base Bx, e esse Bx está inteiramente contido em A, isto é, B_x ⊂ A. O raciocínio inverso também é válido: se todo x em A pertence a algum B_x que, por sua vez, está contido em A, então A é aberto na topologia gerada por B.

Exemplo

Considere \( X = \{1, 2, 3, 4, 5\} \) e uma base para uma topologia em \( X \) dada por \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \). Vamos verificar se \( A = \{1, 2, 3\} \) é aberto.

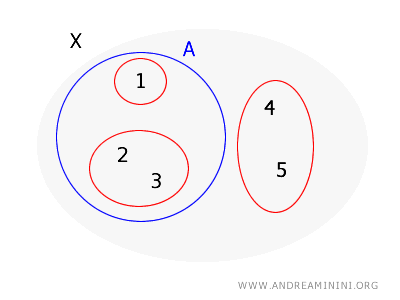
Para cada ponto de \( A \), é preciso encontrar um conjunto da base que o contenha e esteja totalmente dentro de \( A \):

• Para o ponto \( 1 \), existe o conjunto da base \( \{1\} \), que contém \( 1 \) e está inteiramente em \( A \).
• Para o ponto \( 2 \), o conjunto da base \( \{2, 3\} \) contém \( 2 \) e está totalmente em \( A \).
• Para o ponto \( 3 \), o mesmo conjunto da base \( \{2, 3\} \) contém \( 3 \) e está inteiramente em \( A \).

Como cada ponto de \( A \) pertence a um conjunto da base que, por sua vez, está contido em \( A \), a condição do teorema é satisfeita.

Portanto, \( A \) é um conjunto aberto na topologia gerada pela base \( B \).

Exemplo 2

Consideremos novamente \( X = \{1, 2, 3, 4, 5\} \) e a base \( B = \{\{1\}, \{2, 3\}, \{4, 5\}\} \) do exemplo anterior.

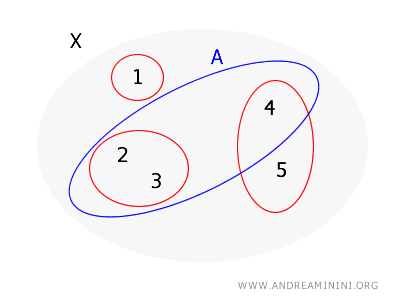
Agora, quero verificar se o conjunto \( A = \{2, 3, 4\} \) é aberto.

• Para o ponto \( 2 \), posso usar o conjunto da base \( \{2, 3\} \), que está inteiramente dentro de \( A \).
• Para o ponto \( 3 \), vale o mesmo conjunto da base \( \{2, 3\} \), que cobre \( 3 \) e está totalmente em \( A \).
• Para o ponto \( 4 \), não existe conjunto da base que o contenha e esteja todo dentro de \( A \), pois o único é \( \{4, 5\} \), que não está contido em \( A \) (já que inclui o 5, que não pertence a \( A \)).

Logo, pelo teorema, o conjunto \( A \) não é aberto na topologia gerada pela base \( B \), pois nem todo ponto de \( A \) possui um conjunto da base totalmente contido nele.

Observações

Algumas observações sobre conjuntos abertos

• Um conjunto A é aberto se, e somente se, A = Int(A)
  Um conjunto \( A \) em um espaço topológico \( X \) é aberto se coincide com seu interior. O interior de A, denotado por Int(A), é a união de todos os conjuntos abertos contidos em \( A \). $$ A = \text{Int}(A) $$

E assim por diante.