A Topologia Usual e os Conjuntos Abertos
A topologia usual (ou padrão) em \( \mathbb{R} \) é construída a partir dos intervalos abertos \( (a, b) \), com \( a < b \). Qualquer união - finita ou infinita - desses intervalos também forma um conjunto aberto. Essa é a maneira mais comum de entender o que significa “aberto” na reta real.
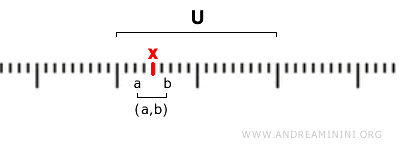
De modo mais rigoroso, um conjunto \( U \) é aberto se, para cada ponto \( x \in U \), existe um intervalo aberto \( (a, b) \) que contém \( x \) e está inteiramente dentro de \( U \):
$$ x \in (a,b) \subseteq U $$
Em outras palavras, em um conjunto aberto, cada ponto tem uma “margem de segurança”: sempre é possível mover-se um pouco para a esquerda e para a direita sem sair do conjunto.
Como identificar conjuntos abertos
Na topologia usual, os conjuntos abertos possuem propriedades bem definidas:
- Intervalos abertos: são os exemplos mais simples - conjuntos da forma \( (a, b) \) com \( a < b \). Qualquer união desses intervalos, seja finita ou infinita, também será um conjunto aberto.
- Operações entre abertos: a união de conjuntos abertos continua sendo aberta, mesmo que envolva infinitos conjuntos. Já a interseção de um número finito de abertos também resulta em um conjunto aberto.
A topologia usual é chamada assim porque é a mais utilizada e a que melhor representa a intuição de “proximidade” e “continuidade” na reta real \( \mathbb{R} \). Ela é fundamental em quase todos os ramos da matemática moderna.
Observação: existem outras topologias possíveis sobre \( \mathbb{R} \) e sobre diferentes espaços. Elas se baseiam em conjuntos-base distintos e produzem noções alternativas de “abertura”. Essas variantes são usadas para estudar propriedades específicas ou para observar as estruturas matemáticas sob outros pontos de vista.
Exemplo prático
A base da topologia usual em \( \mathbb{R} \) é o conjunto de todos os intervalos abertos \( (a, b) \) com \( a < b \):
$$ B = \{ (a,b) \subset \mathbb{R} \ | \ a<b \} $$
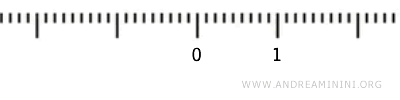
Para qualquer ponto \( x \) que pertença a um conjunto aberto \( U \), sempre existe um intervalo aberto centrado em \( x \) e completamente contido em \( U \):
$$ \forall \ x \in U \ \exists \ \epsilon>0 \ | \ (x-\epsilon, x+\epsilon) \subseteq U $$
Essa propriedade é o coração da definição de conjunto aberto. É o que garante que, dentro de \( U \), não há fronteiras “duras” - podemos nos mover sem sair dele.
Chamamos essa topologia de “usual” porque ela é usada para formalizar, de modo preciso, ideias intuitivas como continuidade, limite e vizinhança.
Exemplo 2: o intervalo (0,1)
Consideremos o intervalo \( (0,1) \), que exclui as extremidades \( 0 \) e \( 1 \). Queremos entender como ele se comporta dentro da topologia usual.
No contexto da topologia induzida, um subconjunto \( U \subset (0, 1) \) é aberto se, para cada ponto \( x \in U \), existe um intervalo aberto \( (a, b) \) em \( \mathbb{R} \) tal que \( x \in (a, b) \) e \( (a, b) \cap (0,1) \subseteq U \).
Isso significa que \( (0,1) \) herda naturalmente uma estrutura topológica bem definida, derivada da topologia usual de \( \mathbb{R} \).
Conclusão: o intervalo \( (0,1) \) é um espaço topológico com a topologia induzida pela topologia padrão da reta real.
Por exemplo, intervalos como \( (0.1, 0.5) \), \( (0.2, 0.9) \) ou a união \( (0.1, 0.5) \cup (0.6, 0.8) \) são abertos em \( (0,1) \). Em termos práticos, os abertos de \( (0,1) \) são exatamente os conjuntos abertos de \( \mathbb{R} \) cuja interseção com \( (0,1) \) permanece contida nesse intervalo.
Como \( (0,1) \) é um subespaço de \( \mathbb{R} \), ele conserva todas as suas propriedades topológicas fundamentais.
Exemplo 3: um conjunto finito
Agora, tomemos o conjunto finito \( X = \{1,2,3\} \), formado por três números naturais. Podemos equipá-lo com uma topologia derivada da topologia usual de \( \mathbb{R} \)?
Não diretamente. A base da topologia padrão é feita de intervalos abertos, e isso não se ajusta a conjuntos finitos e discretos como \( X \).
Por exemplo, o elemento \( \{2\} \) pode ser incluído num intervalo aberto \( (2-\epsilon, 2+\epsilon) \), mas esse intervalo contém infinitos números reais que não pertencem a \( X \). Assim, \( \{2\} \) não é um conjunto aberto na topologia usual de \( \mathbb{R} \).
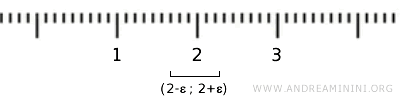
Se considerarmos \( X \) como um subconjunto de \( \mathbb{R} \), a chamada topologia induzida em \( X \) conterá apenas dois conjuntos abertos: o conjunto vazio e o próprio \( X \). É o caso mais simples possível - uma topologia trivial.
Para atribuir uma estrutura mais interessante a conjuntos finitos, os matemáticos recorrem à topologia discreta, onde todo subconjunto é considerado aberto por definição. Essa escolha torna o estudo mais flexível e permite explorar propriedades específicas.
Esses exemplos mostram como a noção de abertura - algo aparentemente simples - pode assumir significados diferentes, dependendo da topologia escolhida. É justamente essa diversidade que torna a topologia uma das áreas mais fascinantes da matemática moderna.