Puntos Fijos en Topología
En topología, un punto fijo es un valor que permanece inmutable bajo la acción de una función.
De manera más directa: si tenemos una función f(x), decimos que p es un punto fijo cuando se cumple que f(p) = p. Es decir, en p la función devuelve exactamente el mismo valor que recibe como entrada.
$$ f(p) = p $$
Un ejemplo intuitivo es la rotación de una figura alrededor de un punto central P.
Al girar el objeto, las coordenadas de todos sus puntos cambian, excepto las del centro de rotación P, que permanecen idénticas.
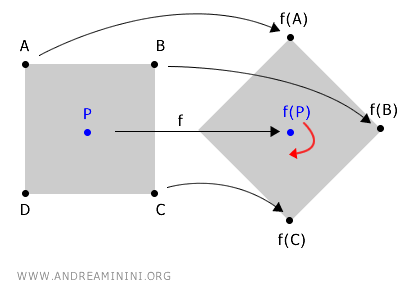
En este caso, el centro P actúa como punto fijo, ya que sus coordenadas no se modifican bajo la rotación, es decir, f(P) = P.
$$ f(P) \longrightarrow P $$
Los puntos fijos son una herramienta fundamental en diversas ramas de las matemáticas y sus aplicaciones, desde el análisis numérico hasta la teoría de juegos y la economía.
En topología, uno de los resultados más célebres relacionados con ellos es el Teorema del Punto Fijo de Brouwer.
Un ejemplo práctico
Consideremos la función f(x) = sin(x) en el intervalo cerrado [0, 2π].
$$ f(x) = \sin(x) $$
En p = 0 radianes encontramos un punto fijo evidente, ya que sin(0) = 0.
$$ \sin(0) = 0 $$
Aquí, la entrada y la salida coinciden exactamente.
Ejemplo 2
Ahora consideremos la función f(x) = cos(x) en el mismo intervalo [0, 2π].
$$ f(x) = \cos(x) $$
En este caso, x = 0 no es un punto fijo, pues cos(0) = 1, lo que evidencia la diferencia entre entrada y salida.
No obstante, la función posee un punto fijo aproximadamente en x ≈ 0.73908513.
$$ \cos(0.73908513) \approx 0.73908513 $$
En ese valor, la función se “encuentra consigo misma”, devolviendo prácticamente el mismo número que recibe.
El Teorema del Punto Fijo de Brouwer
El teorema establece lo siguiente:
Toda función continua que mapea un conjunto compacto y convexo de dimensión n en sí mismo tiene al menos un punto fijo.
Se trata de un resultado de existencia: garantiza la presencia de un punto fijo, aunque no precise su ubicación.
Este principio tiene profundas implicaciones, en particular en la demostración de la existencia de equilibrios en sistemas dinámicos, en modelos económicos y en numerosas áreas de la matemática aplicada.
Y así sucesivamente.