Topologia Numérica (Digital)
A topologia digital (digital topology) é um ramo da topologia que se dedica ao estudo de estruturas definidas em espaços discretos, como grades de pontos, pixels em duas dimensões ou voxels em três dimensões. Seu objetivo é descrever, de forma rigorosa, como esses elementos se conectam entre si a partir de uma noção bem estabelecida de adjacência.
Nesse contexto, os conjuntos abertos não são definidos por intervalos contínuos, como na topologia clássica, mas sim pelas ligações efetivas entre os pontos. O tipo de conectividade adotado depende do modelo considerado, como a conectividade 4 ou 8 em duas dimensões, ou ainda a conectividade 6, 18 ou 26 em três dimensões.
A topologia digital é amplamente utilizada em áreas como processamento de imagens, computação gráfica e visão computacional, pois permite adaptar conceitos fundamentais da topologia clássica a ambientes discretos e computacionais, típicos das representações digitais.
Conjuntos Abertos em Topologia Digital
Em topologia digital, um conjunto \(U\) é dito aberto se, para todo ponto \(x \in U\), todos os pontos adjacentes a \(x\), de acordo com a regra de conectividade adotada, também pertencem a \(U\).
A noção de adjacência, ou de vizinhança, entre pontos varia conforme o tipo de conectividade escolhido no espaço digital. Alguns exemplos ajudam a tornar essa ideia mais concreta.
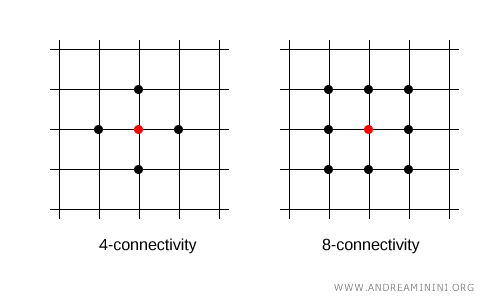
Em uma grade circular ou anelar, cada ponto é adjacente exatamente a outros dois. Esse tipo de estrutura corresponde a uma conectividade 2.
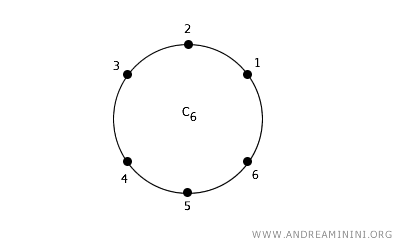
Em um plano bidimensional, um ponto pode estar ligado a quatro vizinhos, conectividade 4, localizados nas direções norte, sul, leste e oeste. Também é possível considerar oito vizinhos, conectividade 8, quando se incluem as diagonais.
Em um espaço digital tridimensional, a conectividade entre os pontos pode seguir critérios de conectividade 6, 18 ou 26, dependendo de quantos vizinhos são considerados relevantes.
Exemplo
Consideremos um conjunto de pontos dispostos em forma de círculo, em um espaço discreto, com conectividade 2.
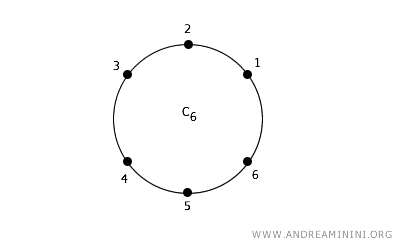
Nessa situação, cada ponto possui dois vizinhos imediatos, um à esquerda e outro à direita.
Por exemplo, o ponto 2 é adjacente aos pontos 1 e 3.

Um conjunto \(U\) é, portanto, aberto em topologia digital se todos os vizinhos de cada ponto pertencente a \(U\) também fizerem parte de \(U\).
Essa definição traduz, em um contexto discreto, a ideia intuitiva de continuidade e de ligação estrutural entre os pontos.
Diferença entre Topologia Digital e Topologia Discreta
Embora a topologia digital e a topologia discreta sejam ambas definidas sobre espaços discretos, elas diferem de maneira conceitual.
- Topologia Discreta
Uma topologia definida sobre um conjunto \(X\) é dita discreta quando todo subconjunto de \(X\) é aberto, sem qualquer restrição adicional. - Topologia Digital
Na topologia digital, um subconjunto só é considerado aberto se respeitar as condições de conectividade impostas entre os pontos.
Qual é, então, a diferença essencial?
Na topologia discreta, qualquer subconjunto é automaticamente aberto. Já na topologia digital, apenas os conjuntos que satisfazem critérios específicos de conectividade são considerados abertos.
Em outras palavras, a topologia digital não é equivalente à topologia discreta, pois nem todos os subconjuntos são automaticamente abertos.
Por exemplo, um conjunto formado por dois pixels isolados, sem qualquer relação de adjacência entre eles, não é aberto em topologia digital, embora seja aberto em uma topologia discreta.
Em síntese, a topologia digital foi desenvolvida para formalizar a noção de conectividade entre pontos em um espaço computacional discreto, enquanto a topologia discreta trata cada ponto como uma entidade isolada, sem levar em conta relações de adjacência.
Exemplo
Consideremos o conjunto de pontos \(\{1, 2, 3, 4\}\) dispostos em círculo, com uma topologia digital baseada em conectividade 2.
- O conjunto \(\{1, 2\}\) é aberto em topologia digital, pois os pontos 1 e 2 são adjacentes.
- O conjunto \(\{1, 3\}\) não é aberto, pois os pontos 1 e 3 não são diretamente adjacentes.
Se analisarmos esses mesmos pontos \(\{1, 2, 3, 4\}\) no contexto de uma topologia discreta, tanto \(\{1, 2\}\) quanto \(\{1, 3\}\) seriam conjuntos abertos, já que, nesse caso, todo subconjunto é aberto.
Observação. Nesse mesmo espaço métrico discreto \(\{1, 2, 3, 4\}\), a topologia digital é mais restritiva do que a topologia discreta, pois impõe uma condição adicional de conectividade para que um conjunto seja considerado aberto.
E assim por diante.