Topologia Produto de Espaços Topológicos

Dados dois espaços topológicos $X$ e $Y$, a topologia produto em $X \times Y$ é a topologia gerada pela base $B$, composta pelos produtos cartesianos de conjuntos abertos da forma $U \times V$, onde $U$ é um aberto de $X$ e $V$ é um aberto de $Y$. $$ B = \{ U \times V \mid U \text{ é aberto em } X \text{ e } V \text{ é aberto em } Y \} $$

Para definir uma topologia em $X \times Y$, começa-se pelos conjuntos mais simples possíveis, isto é, os produtos $U \times V$, onde cada fator é um aberto do espaço correspondente.

O conjunto de todos esses produtos, indicado por $B$, forma uma base de uma topologia.

De modo geral, chama-se base topológica qualquer coleção de conjuntos abertos tal que todo aberto do espaço possa ser escrito como união de elementos dessa coleção.

Na topologia produto, vale uma propriedade fundamental: o produto cartesiano de dois conjuntos abertos é novamente um conjunto aberto.

Observação : Os abertos da topologia produto não se limitam aos produtos cartesianos $U \times V$. Eles incluem também todas as uniões possíveis desses produtos. Por esse motivo, o conjunto $B$ não é uma topologia completa, mas apenas uma base. Se $B$ fosse considerado como uma topologia em si, muitos abertos legítimos ficariam de fora.

Um raciocínio semelhante vale para os conjuntos fechados.

Na topologia produto, o produto cartesiano de dois conjuntos fechados é também um conjunto fechado.

No entanto, nem todo conjunto fechado da topologia produto pode ser representado como um produto cartesiano de fechados.

Assim como ocorre com os abertos, existem conjuntos fechados na topologia produto que não resultam diretamente de um produto cartesiano.

Um Exemplo Concreto
Produto de Vários Espaços Topológicos
Base da Topologia Produto
Observações Finais

Um Exemplo Concreto

Vejamos agora um exemplo simples para tornar essa construção mais intuitiva.

Considere os seguintes espaços topológicos:

$X$ é a reta real $\mathbb{R}$, munida da sua topologia usual, cujos abertos são os intervalos abertos $(a, b)$.
$Y$ é também \(\mathbb{R}\/pt/math/associatividade-do-produto-cartesiano-de-espaos-topologicos), com a mesma topologia usual.

Nesse caso, o produto $X \times Y$ coincide com o plano cartesiano $\mathbb{R}^2$.

A base $B$ da topologia produto em $X \times Y$ é formada por todos os conjuntos do tipo $U \times V$, onde $U$ e $V$ são intervalos abertos da reta real.

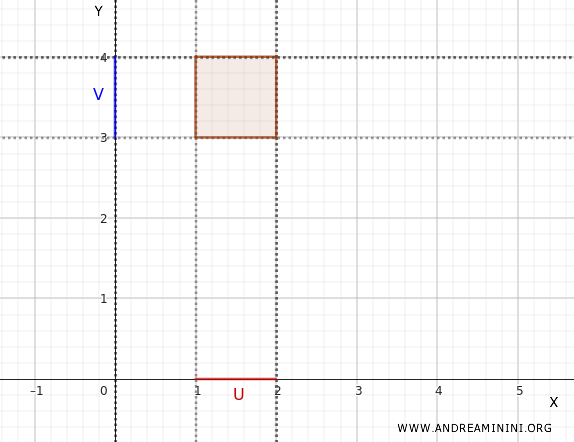
Por exemplo, seja $U = (1, 2) \subset X$.

E seja $V = (3, 4) \subset Y$.

Então, o conjunto $U \times V = (1, 2) \times (3, 4)$ é um aberto de $\mathbb{R}^2$. Geometricamente, ele corresponde a um retângulo aberto no plano cartesiano.

retângulo aberto no plano cartesiano

Consideremos agora a união de dois conjuntos da base.

Tomemos $U_1 \times V_1 = (1, 2) \times (3, 4)$.

E $U_2 \times V_2 = (1.5, 2.5) \times (3.5, 4.5)$.

Ambos representam retângulos abertos no plano.

união de retângulos abertos no plano

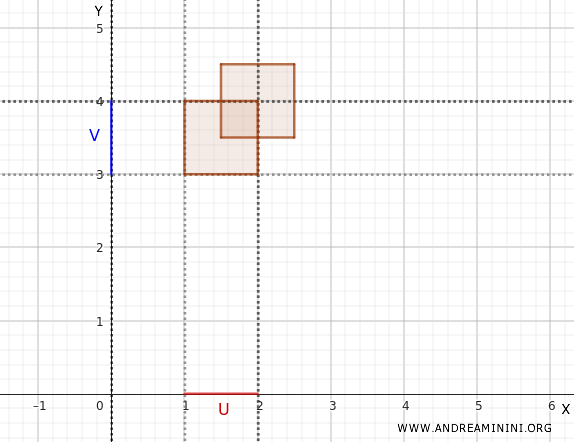
A união desses dois conjuntos já não pode ser descrita como um único produto cartesiano. Ainda assim, por ser formada por elementos da base, ela é um aberto da topologia produto:

$$ (1, 2) \times (3, 4) \cup (1.5, 2.5) \times (3.5, 4.5) $$

Isso mostra que todo ponto do plano pertence a algum aberto que pode ser escrito como união de produtos do tipo $U \times V$.

Por exemplo, o ponto $(1.8, 3.8)$ pertence a $ (1, 2) \times (3, 4) $ e, consequentemente, também à união dos dois retângulos.

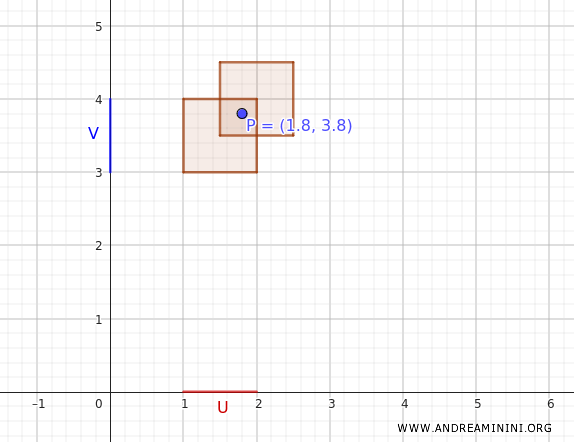
ponto contido na união de abertos da base

Esse exemplo ilustra de forma clara como a base $B$ gera efetivamente a topologia produto sobre $X \times Y$.

Observação : A topologia produto é especialmente importante porque permite construir espaços maiores preservando a estrutura topológica dos espaços originais.

Exemplo 2

Consideremos agora dois espaços topológicos finitos:

$X = \{a, b, c\}$, com a topologia $\{\emptyset, \{a\}, \{b, c\}, X\}$
$Y = \{1, 2\}$, com a topologia $\{\emptyset, \{1\}, Y\}$

Para determinar a topologia produto em $X \times Y$, calculam-se todos os produtos cartesianos entre abertos de $X$ e de $Y$, e em seguida consideram-se todas as uniões possíveis desses conjuntos.

$$ B = \{ U \times V \mid U \text{ é aberto em } X \text{ e } V \text{ é aberto em } Y \} $$

Os abertos de $X$ são:

$\emptyset$
$\{a\}$
$\{b, c\}$
$X = \{a, b, c\}$

Os abertos de $Y$ são:

$\emptyset$
$\{1\}$
$Y = \{1, 2\}$

A seguir, listamos os produtos cartesianos correspondentes:

$\emptyset \times \emptyset = \emptyset$
$\emptyset \times \{1\} = \emptyset$
$\emptyset \times Y = \emptyset$
$\{a\} \times \emptyset = \emptyset$
$\{a\} \times \{1\} = \{(a, 1)\}$
$\{a\} \times Y = \{(a, 1), (a, 2)\}$
$\{b, c\} \times \emptyset = \emptyset$
$\{b, c\} \times \{1\} = \{(b, 1), (c, 1)\}$
$\{b, c\} \times Y = \{(b, 1), (b, 2), (c, 1), (c, 2)\}$
$X \times \emptyset = \emptyset$
$X \times \{1\} = \{(a, 1), (b, 1), (c, 1)\}$
$X \times Y = \{(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)\}$

Observação : O produto cartesiano de dois conjuntos é definido como o conjunto de todos os pares ordenados $(a, b)$ tais que $a \in A$ e $b \in B$. Se um dos conjuntos for vazio, o produto cartesiano também será vazio.

A topologia produto em $X \times Y$ é formada por todas as uniões possíveis dos conjuntos acima.

Isso mostra que, na topologia produto, os abertos não se restringem aos produtos simples $U \times V$. As uniões desses produtos também são conjuntos abertos.

Por exemplo, $\{(a, 1)\} \cup \{(b, 1), (c, 1)\} = \{(a, 1), (b, 1), (c, 1)\}$ é um aberto da topologia produto.

A base $B$ da topologia em $X \times Y$ é composta exclusivamente pelos produtos cartesianos não vazios.

Produto de Vários Espaços Topológicos

O conceito de topologia produto estende-se de forma natural ao caso do produto de vários espaços topológicos.

Dados $ n $ espaços topológicos $ X_1, X_2, \dots, X_n $, se para cada índice $ i $ for escolhido um aberto $ U_i \subseteq X_i $, então o conjunto de todos os produtos cartesianos $ U_1 \times U_2 \times \cdots \times U_n $ constitui uma base para uma topologia no espaço produto $ X_1 \times \cdots \times X_n $. $$ B = \{ U_1 \times U_2 \times \cdots \times U_n \mid U_i \text{ é aberto em } X_i \text{ para todo } i \} $$

Base da Topologia Produto

De modo geral, o produto cartesiano de conjuntos abertos provenientes de dois espaços topológicos fornece uma base válida para a topologia produto.

$$ B = \{ U \times V \mid U \text{ é aberto em } X,\ V \text{ é aberto em } Y \} $$

Essa descrição é conceitualmente simples, mas pode tornar-se rapidamente muito extensa, sobretudo quando os espaços envolvidos possuem muitos abertos.

Felizmente, existe um método alternativo, mais enxuto e igualmente rigoroso, para construir uma base da topologia produto.

Se $ B_X $ é uma base da topologia de $ X $ e $ B_Y $ é uma base da topologia de $ Y $, então o conjunto de todos os produtos $ U \times V $, com $ U \in B_X $ e $ V \in B_Y $, forma uma base da topologia produto em $ X \times Y $: $$ B = \{ U \times V \mid U \in B_X,\ V \in B_Y \} $$

Esse conjunto $ B $ é suficiente para gerar toda a topologia produto sobre $ X \times Y $.

Em termos intuitivos, os elementos de $ B $ funcionam como os “blocos básicos” da topologia produto. Qualquer conjunto aberto nesse espaço pode ser obtido como união de produtos cartesianos desse tipo.

Observação : Essa construção generaliza-se naturalmente ao caso de produtos finitos. Dados $ n $ espaços topológicos $ X_1, X_2, \dots, X_n $, se $ B_i $ é uma base da topologia de $ X_i $, então o conjunto dos produtos $ U_1 \times U_2 \times \cdots \times U_n $, com $ U_i \in B_i $, constitui uma base da topologia produto em $ X_1 \times \cdots \times X_n $: $$ B = \{ U_1 \times \cdots \times U_n \mid U_i \in B_i,\ i = 1, \dots, n \} $$

Exemplo

Consideremos dois espaços topológicos finitos:

O espaço $ X = \{a, b\} $, munido da topologia $ \mathcal{T}_X = \{\emptyset, \{a\}, \{b\}, \{a, b\}\} $, cuja base mínima é $ B_X = \{\{a\}, \{b\}\} $.
O espaço $ Y = \{1, 2\} $, munido da topologia $ \mathcal{T}_Y = \{\emptyset, \{1\}, \{2\}, \{1, 2\}\} $, cuja base mínima é $ B_Y = \{\{1\}, \{2\}\} $.

Para obter uma base mínima da topologia produto, basta considerar os produtos cartesianos entre os elementos de $ B_X $ e $ B_Y $, sem necessidade de listar todos os abertos de $ X $ e de $ Y $.

$$ B_X = \{\{a\}, \{b\}\}, \quad B_Y = \{\{1\}, \{2\}\} $$

Os produtos cartesianos correspondentes são:

$$ \{a\} \times \{1\} = \{(a, 1)\}, \quad \{a\} \times \{2\} = \{(a, 2)\} $$

$$ \{b\} \times \{1\} = \{(b, 1)\}, \quad \{b\} \times \{2\} = \{(b, 2)\} $$

Assim, uma base mínima da topologia produto em $ X \times Y $ é:

$$ B_{\text{min}} = \{\{(a, 1)\}, \{(a, 2)\}, \{(b, 1)\}, \{(b, 2)\}\} $$

Mesmo sendo composta por poucos conjuntos, essa base é suficiente para gerar toda a topologia produto em $ X \times Y $.

Em resumo, ao trabalhar diretamente com conjuntos básicos, isto é, produtos de abertos das bases originais, obtém-se uma descrição simples, eficiente e completa da topologia produto.

Demonstração

Mostremos agora que o conjunto $ B = \{U \times V \mid U \in B_X,\ V \in B_Y\} $ constitui, de fato, uma base da topologia produto em $ X \times Y $.

Por hipótese, $ B_X $ e $ B_Y $ são bases das topologias de $ X $ e de $ Y $, respectivamente.

Recorde-se que, por definição, na topologia produto os conjuntos abertos são uniões de conjuntos da forma $ U \times V $, onde $ U \subseteq X $ e $ V \subseteq Y $ são abertos.

Para verificar que $ B $ é uma base, basta demonstrar que todo aberto $ W \subseteq X \times Y $ pode ser escrito como união de elementos de $ B $.

Verificação da propriedade de base

Seja $ W $ um aberto da topologia produto e seja $ (x, y) \in W $.

Pela própria definição da topologia produto, existe um conjunto aberto elementar $ U' \times V' \subseteq W $, com $ U' \subseteq X $ e $ V' \subseteq Y $ abertos, tal que:

$$ (x, y) \in U' \times V' \subseteq W $$

Como $ B_X $ é uma base da topologia de $ X $, existe $ U \in B_X $ tal que $ x \in U \subseteq U' $. De modo análogo, como $ B_Y $ é uma base da topologia de $ Y $, existe $ V \in B_Y $ tal que $ y \in V \subseteq V' $.

Segue-se então que:

$$ (x, y) \in U \times V \subseteq U' \times V' \subseteq W $$

Isso mostra que, para todo ponto de $ W $, existe um elemento da base $ B $ que o contém e que está contido em $ W $.

Conclusão

Como todo ponto de $ W $ pertence a algum conjunto da base $ B $ contido em $ W $, conclui-se que $ B $ gera efetivamente a topologia produto.

Portanto, o conjunto $ B = \{U \times V \mid U \in B_X,\ V \in B_Y\} $ satisfaz todas as condições necessárias para ser uma base da topologia produto em $ X \times Y $.

A demonstração fica, assim, concluída.

Observações Finais

Encerramos com alguns resultados clássicos e frequentemente utilizados no estudo da topologia produto:

Teorema do Subespaço Produto
Se $ A \subseteq X $ e $ B \subseteq Y $ são subespaços topológicos, então a topologia induzida em $ A \times B $, considerada como subespaço de $ X \times Y $, coincide com a topologia produto construída a partir das topologias de subespaço de $ A $ e de $ B $: $$ \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Equivalência Topológica dos Produtos
Dados três espaços topológicos $ X, Y, Z $, os espaços $ (X \times Y) \times Z $, $ X \times (Y \times Z) $ e $ X \times Y \times Z $ são homeomorfos. Em outras palavras, a forma de parentetização não altera a estrutura topológica do produto: $$ (X \times Y) \times Z \cong X \times (Y \times Z) \cong X \times Y \times Z $$
Teorema do Interior de um Produto Cartesiano
Para subconjuntos $ A \subseteq X $ e $ B \subseteq Y $, o interior do produto cartesiano coincide com o produto dos interiores correspondentes: $$ \text{Int}(A \times B) = \text{Int}(A) \times \text{Int}(B) $$