Teorema do Subespaço do Produto de Espaços Topológicos
Sejam \(A\) e \(B\) dois subconjuntos, respetivamente, dos espaços topológicos \(X\) e \(Y\), $$ A \subset X $$ $$ B \subset Y $$ a topologia definida no produto \(A \times B\), quando este é considerado como subespaço de \(X \times Y\), coincide exatamente com a topologia produto em \(A \times B\), construída a partir das topologias induzidas em \(A\) e \(B\) pelos espaços \(X\) e \(Y\): $$ \tau_{A \times B}^{\text{sub}} = \tau_A^{\text{sub}} \times \tau_B^{\text{sub}} $$
Neste contexto, \(\tau_{A \times B}^{\text{sub}}\) designa a topologia de subespaço em \(A \times B\), induzida pela topologia do espaço produto \(X \times Y\).
De modo análogo, \(\tau_A^{\text{sub}}\) e \(\tau_B^{\text{sub}}\) representam as topologias de subespaço em \(A\) e \(B\), obtidas por restrição das topologias de \(X\) e \(Y\), respetivamente.
O teorema estabelece que essas duas formas de construção conduzem exatamente à mesma estrutura topológica em \(A \times B\).
Em termos práticos, isso significa que considerar \(A \times B\) como subespaço de \(X \times Y\) ou formar diretamente o produto das topologias induzidas em \(A\) e \(B\) leva ao mesmo resultado.
Independentemente do caminho seguido, a topologia final em \(A \times B\) é a mesma.
Um Exemplo Concreto
Para tornar essa afirmação mais intuitiva, vejamos um exemplo simples e concreto.
Consideremos dois espaços topológicos \(X\) e \(Y\). Um caso familiar é o do plano cartesiano, em que \(X\) corresponde ao eixo das abcissas e \(Y\) ao eixo das ordenadas.
Sejam \(A \subseteq X\) e \(B \subseteq Y\) dois subconjuntos desses espaços.
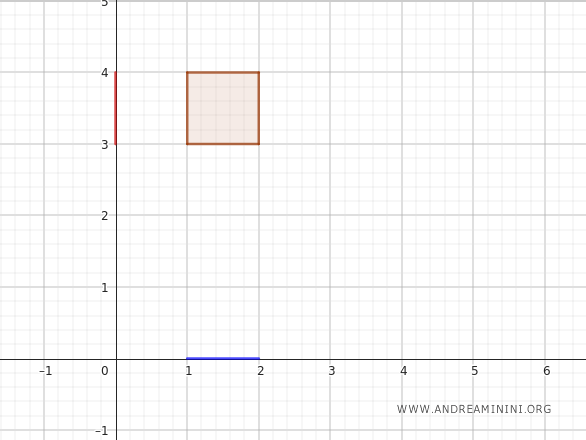
Por exemplo, tomemos \(A = [1, 2]\), um intervalo do eixo \(x\), e \(B = [3, 4]\), um intervalo do eixo \(y\).
O produto cartesiano \(A \times B\) é o conjunto de todos os pares ordenados \((x, y)\) tais que \(x \in A\) e \(y \in B\).
Geometricamente, esse conjunto corresponde a um retângulo do plano, com lados paralelos aos eixos coordenados, em que \(x\) varia entre 1 e 2, e \(y\) varia entre 3 e 4.
Existem duas maneiras naturais de definir uma topologia em \(A \times B\):
- Topologia de subespaço
Considera-se \(A \times B\) como um subconjunto de \(X \times Y\), isto é, do plano completo munido da topologia produto. A topologia em \(A \times B\) é então obtida pela restrição da topologia de \(X \times Y\). - Topologia produto
Alternativamente, atribuem-se a \(A\) e \(B\) as topologias que herdam, respetivamente, de \(X\) e \(Y\), e constrói-se em seguida a topologia produto em \(A \times B\) como o produto dessas topologias induzidas.
O ponto central do teorema é que essas duas construções produzem exatamente a mesma topologia em \(A \times B\).
Assim, qualquer que seja a abordagem adotada, a estrutura topológica final de \(A \times B\) permanece inalterada.
E assim por diante...