A fronteira de um conjunto

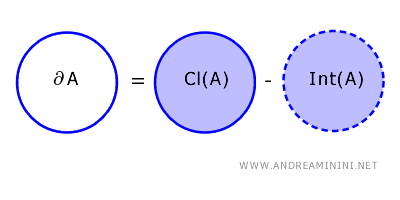
A fronteira de um subconjunto \( A \) de um espaço topológico \( X \) é formada pelos pontos que pertencem à aderência de \( A \), mas não ao seu interior. Em símbolos: \[ \partial A = \text{Cl}(A) - \text{Int}(A) \]

O termo \( \text{Cl}(A) \) indica a aderência, que reúne todos os pontos de \( A \) e os seus pontos de acumulação.

Já \( \text{Int}(A) \) designa o interior de \( A \), isto é, os pontos que dispõem de uma vizinhança totalmente contida no conjunto.

A ideia fundamental é que a fronteira depende da topologia escolhida. Ou seja, não é uma característica fixa do conjunto, mas uma noção relativa ao ambiente topológico em que ele está inserido.

Por isso, o mesmo conjunto pode apresentar fronteiras diferentes em topologias distintas.

Uma forma intuitiva de pensar em \( \partial A \) é: ela contém os pontos que estão ao mesmo tempo "encostados" em \( A \) e no seu complementar \( X \setminus A \).

Um exemplo passo a passo

Tomemos como exemplo o intervalo aberto \( A = (0, 1) \) na reta real \( \mathbb{R} \), com a topologia usual.

1. Aderência de A

A aderência inclui todos os pontos do conjunto e também os seus limites. Para \( A = (0, 1) \), isso resulta no intervalo fechado \([0, 1]\), já que tanto 0 como 1 podem ser atingidos por sequências provenientes de dentro do intervalo.

$$ \text{Cl}(A) = [0, 1] $$

2. Interior de A

O interior reúne os pontos que possuem vizinhanças inteiramente contidas em \( A \). Como o intervalo é aberto, nada muda:

$$ \text{Int}(A) = (0, 1) $$

3. Fronteira de A

A fronteira surge ao retirarmos o interior da aderência:

$$ \partial A = \text{Cl}(A) - \text{Int}(A) $$

Substituindo:

$$ \partial A = [0, 1] - (0, 1) = \{0, 1\} $$

Ou seja, os pontos 0 e 1 formam a fronteira de \( A \). São precisamente os pontos onde o intervalo "acaba", no sentido topológico: qualquer vizinhança desses valores toca tanto o intervalo quanto o lado de fora.

O teorema da fronteira

Um ponto \( x \in X \) está na fronteira de \( A \) se, e somente se, toda vizinhança de \( x \) intersecta simultaneamente o conjunto e o seu complementar.

É um critério prático: se nenhuma vizinhança de \( x \) consegue "ficar apenas de um lado", então \( x \) está na fronteira.

Aplicação ao nosso exemplo

Com \( A = (0, 1) \), temos novamente:

$$ \text{Cl}(A) = [0, 1], \quad \text{Int}(A) = (0, 1), \quad \partial A = \{0, 1\}. $$

Verificando o ponto 0

Qualquer intervalo \( (0 - \epsilon, 0 + \epsilon) \) contém números negativos ou iguais a 0 e ao mesmo tempo valores de \( (0, 1) \). Assim, 0 satisfaz o critério.

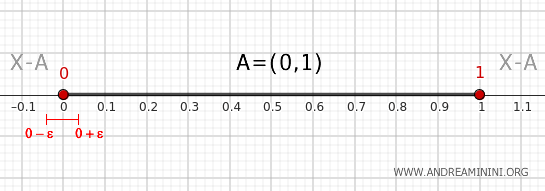
Verificando o ponto 1

De forma análoga, toda vizinhança de 1 contém valores de dentro do intervalo e valores maiores ou iguais a 1, o que garante a interseção dupla.

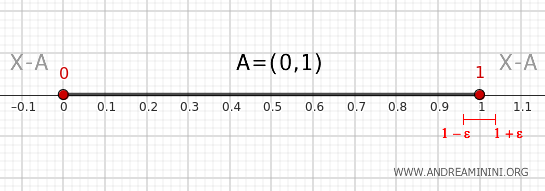
Verificando um ponto interior

Escolhendo, por exemplo, 0,5, todas as vizinhanças estão inteiramente dentro de \( (0,1) \). Não há contato com o exterior.

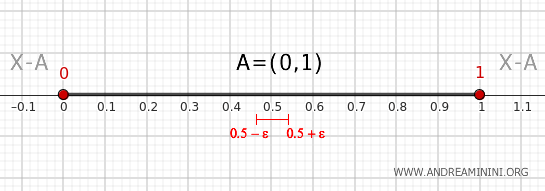
Concluímos que apenas 0 e 1 ficam na fronteira, enquanto pontos como 0,5 estão completamente no interior.

Propriedades importantes

Algumas relações fundamentais envolvendo interior, aderência e fronteira:

• A fronteira está contida em \( A \) se, e somente se, \( A \) é fechado.
  \[ \partial A \subseteq A \Leftrightarrow A \text{ é fechado} \]
• \( A \) é aberto se, e somente se, não compartilha pontos com sua própria fronteira.
  \[ \partial A \cap A = \emptyset \Leftrightarrow A \text{ é aberto} \]
• A fronteira é vazia apenas quando \( A \) é ao mesmo tempo aberto e fechado (clopen).
  \[ \partial A = \emptyset \Leftrightarrow A \text{ é clopen} \]
• A fronteira coincide com a interseção entre a aderência de \( A \) e a do complementar.
  \[ \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \]
• A fronteira é sempre um conjunto fechado.
  

  A interseção de dois fechados resulta sempre em um conjunto fechado. Como \( \partial A = \text{Cl}(A) \cap \text{Cl}(X - A) \), a fronteira é necessariamente fechada.

• A fronteira e o interior nunca se sobrepõem.
  \[ \partial A \cap \text{Int}(A) = \emptyset \]
• A união entre interior e fronteira recupera exatamente a aderência.
  \[ \partial A \cup \text{Int}(A) = \text{Cl}(A) \]

Essas propriedades ajudam a entender como interior, aderência e fronteira se articulam dentro da topologia geral, oferecendo um quadro coerente e útil para o estudo de conjuntos em espaços topológicos.